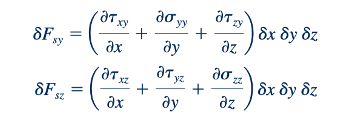Deskripsi Gaya-gaya yang Bekerja pada Elemen Diferensial
Deskripsi gaya-gaya yang bekerja pada elemen diferensial. Secara umum, dua jenis gaya perlu dipertimbangkan: gaya permukaan, yang bekerja pada permukaan elemen diferensial, dan gaya benda, yang didistribusikan di seluruh elemen. Untuk tujuan kita, satu-satunya gaya benda, 𝛿Fb , yang menarik adalah berat dari elemen, yang dapat diungkapkan sebagai
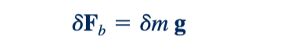
di mana g adalah representasi vektor dari percepatan gravitasi. Dalam bentuk komponen, persamaannya menjadi:
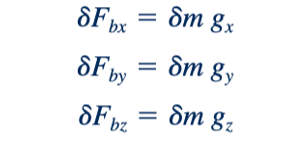
dimana gx , gy , dan gz adalah komponen vektor percepatan gravitasi dalam arah x, y, dan z, masing-masing.
Gaya permukaan bertindak pada elemen sebagai akibat interaksinya dengan lingkungannya. Pada lokasi sembarang dalam massa fluida, gaya yang bertindak pada suatu area kecil, 𝛿A, yang terletak dalam suatu permukaan sembarang, dapat diwakili oleh 𝛿Fs , seperti yang ditunjukkan dalam Gambar 6.9. Secara umum, dF s akan miring terhadap permukaan. Gaya 𝛿Fs dapat diuraikan menjadi tiga komponen, 𝛿Fn ,𝛿F1 , dan 𝛿F2 , di mana 𝛿Fn adalah tegak lurus terhadap area, 𝛿A, dan 𝛿F1 dan 𝛿F2 sejajar dengan area dan ortogonal satu sama lain. Tegangan normal, σn , didefinisikan sebagai:
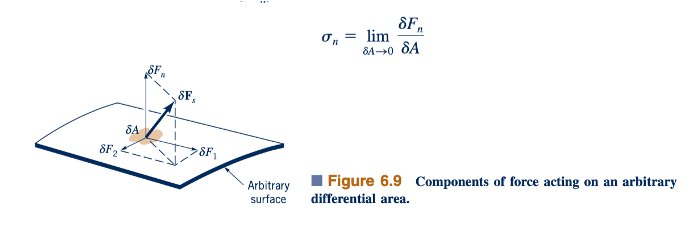
dan tegangan geser didefinisikan sebagai:

Dan
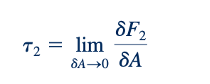
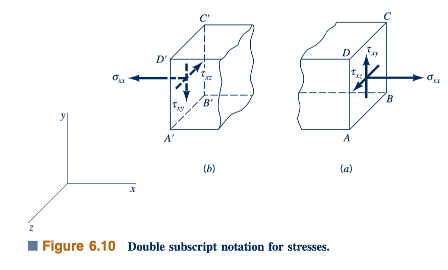
Kami akan menggunakan s untuk tegangan normal dan t untuk tegangan geser. Intensitas gaya per satuan luas pada suatu titik dalam suatu benda dapat dikarakterisasi oleh tegangan normal dan dua tegangan geser, jika orientasi area tersebut ditentukan. Untuk tujuan analisis, biasanya nyaman untuk merujuk area ke sistem koordinat. Sebagai contoh, untuk sistem koordinat segiempat yang ditunjukkan dalam Gambar 6.10, kita memilih untuk mempertimbangkan tegangan yang bekerja pada bidang yang paralel dengan bidang koordinat. Pada bidang ABCD pada Gambar 6.10a, yang paralel dengan bidang y−z, tegangan normal dinotasikan sebagai σ xx dan tegangan geser dinotasikan sebagai τ xy dan τ xz. Untuk dengan mudah mengidentifikasi komponen tegangan tertentu, kami menggunakan notasi subskrip ganda. Subskrip pertama menunjukkan arah normal terhadap bidang di mana tegangan bertindak, dan subskrip kedua menunjukkan arah tegangan. Dengan demikian, tegangan normal memiliki subskrip yang diulang, sedangkan subskrip untuk tegangan geser selalu berbeda.
Juga perlu untuk menetapkan konvensi tanda untuk tegangan. Kami mendefinisikan arah positif untuk tegangan sebagai arah koordinat positif pada permukaan di mana normal keluar berada dalam arah koordinat positif. Ini adalah kasus yang diilustrasikan dalam Gambar 6.10a di mana normal keluar dari area ABCD berada dalam arah positif x. Arah positif untuk σ xx, τ xy , dan τ xz seperti yang ditunjukkan dalam Gambar 6.10a. Jika normal keluar menunjuk ke arah koordinat negatif, seperti pada Gambar 6.10b untuk area A'B'C'D', maka tegangan dianggap positif jika ditujukan ke arah koordinat negatif. Dengan demikian, tegangan yang ditunjukkan dalam Gambar 6.10b dianggap positif ketika ditunjukkan. Perhatikan bahwa tegangan normal positif adalah tegangan tarik; yaitu, mereka cenderung "meregangkan" material.
Perlu ditekankan bahwa keadaan tegangan di suatu titik dalam bahan tidak sepenuhnya ditentukan hanya dengan tiga komponen dari "vektor tegangan". Ini mengikuti, karena vektor tegangan tertentu bergantung pada orientasi bidang yang melewati titik tersebut. Namun, dapat ditunjukkan bahwa tegangan normal dan geser yang bertindak pada setiap bidang yang melewati suatu titik dapat dinyatakan dalam hal tegangan yang bertindak pada tiga bidang ortogonal yang melewati titik (Lihat Referensi 22).
Sekarang kita dapat menyatakan gaya permukaan yang bertindak pada suatu elemen kubus kecil fluida dalam hal tegangan yang bertindak pada permukaan elemen seperti yang ditunjukkan dalam Gambar 6.11. Diharapkan bahwa pada umumnya tegangan akan bervariasi dari titik ke titik dalam medan aliran. Dengan demikian, melalui penggunaan ekspansi deret Taylor, kita akan menyatakan tegangan pada berbagai permukaan dalam hal tegangan yang sesuai di pusat elemen Gambar 6.11 dan gradiennya dalam arah koordinat. Untuk kesederhanaan, hanya gaya dalam arah x yang ditunjukkan. Perhatikan bahwa tegangan harus dikalikan dengan luas tempat mereka bertindak untuk mendapatkan gaya. Menjumlahkan semua gaya ini dalam arah x menghasilkan

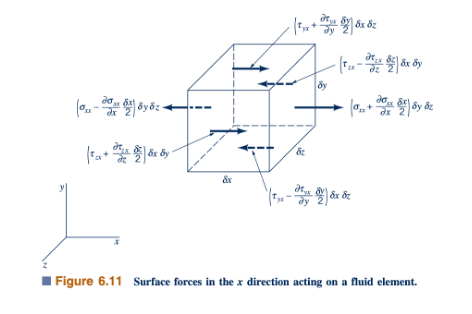
untuk gaya permukaan resultan dalam arah x. Dengan cara yang serupa, gaya permukaan resultan dalam arah y dan z dapat diperoleh dan diungkapkan sebagai