2.3.3 Determinan dari Matriks Persegi

Determinan dari matriks persegi. Determinan adalah nilai yang terkait dengan matriks persegi A yang dapat dihitung dari elemen-elemen matriks tersebut melalui prosedur matematika, dan dinyatakan sebagai det(A) atau |A| (yang tidak boleh disalahartikan dengan notasi nilai mutlak) [13]. Perhitungan determinan matriks orde 2 sangatlah langsung dan merupakan hasil kali elemen-elemen pada diagonal utama dikurangi hasil kali elemen-elemen pada diagonal silang. Jika A adalah matriks persegi berorde 2, maka:

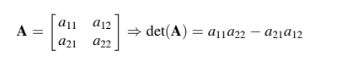
Untuk matriks berorde lebih tinggi, prosedurnya lebih rumit dan didasarkan pada konsep minor dan koefaktor. Sebuah minor (mi)ij untuk elemen $a_{ij}$ adalah determinan yang dihasilkan ketika baris ke-i dan kolom ke-j dihapus. Koefaktor ( $co)_{ij}$ dari elemen $a_{ij}$ adalah nilai minor dikalikan dengan tanda positif atau negatif tergantung pada apakah (i + j) genap atau ganjil, secara berturut-turut. Hubungan matematika antara koefaktor dan minor dapat dituliskan sebagai berikut:

Determinan dari matriks persegi A berorde N dihitung dengan mencari koefaktor dari salah satu baris atau kolomnya, mengalikan setiap koefaktor dengan elemen yang sesuai, dan menjumlahkan hasilnya. Secara matematis, ini dinyatakan sebagai berikut:

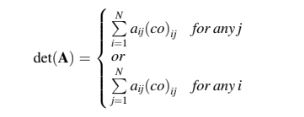
Harus dijelaskan bahwa perhitungan koefaktor dapat memerlukan dekomposisi lebih lanjut dari determinan minor. Dekomposisi ini dapat menghasilkan dekomposisi lebih lanjut hingga mencapai determinan dengan ukuran 2. Selain itu, berdasarkan diskusi di atas, dapat dengan mudah ditunjukkan bahwa determinan dari matriks segitiga atas, segitiga bawah, atau diagonal A berorde N adalah hasil kali dari elemen-elemen sepanjang diagonal utamanya, yaitu: