Bagian ini membahas dinamika fluida dalam konteks CFD. Topik  yangbahas meliputi persamaan dasar (governing equation) seperti konservasi massa, momentum dan energi, serta model fisika fluida seperti viskositas, konduktivitas termal (conductivity thermal) dan termodinamika.

Persamaan-persamaan ini menggambarkan gerakan fluida, gaya dan perpindahan panas dalam waktu dan ruang 3D. Notasi vektor menyediakan kerangka matematika untuk menyajikan persamaan dalam bentuk kompak. Metode ini memungkinkan persamaan disajikan secara independen dari sistem koordinat manapun, misalnya koordinat kartesian (x, y, z). atau koordinat speris (lingkaran), (r, 𝜃, 𝜑). Persamaan ini juga termasuk seperangkat operator aljabar standar, misalnyna produk dalam dot dan produk luar

Notasi ini membantu memastikan bahwa istilah dalam persamaan tidak berubah atau invarian, dalam transformasi sistem koordinat. Tanpa invarian, solusi aliran, misalnya sepanjang pipa, akan bergantung pada orientasi pipa terhadap sistem koordinat. Secara logis, ketergantungan ini diabaikan; hukum geraknya sama dalam semua “kerangka inersial.”

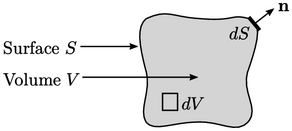
Derivative dari governing equation menggunakan control volume V yang dibatasi oleh suatu permukaan S, disajikan menggunakan ilustrasi 2D di atas. Kami menggunakan dV dan dS untuk menggambarkan volume dan permukaan yang tak terhingga kecilnya, secara berturut-turut, dan n adalah vektor normal satuan untuk setiap penambahan permukaan dS, dibahas dalam bagian 2.1. Penting untuk dicatat dalam setiap turunan apakah volume didefinisikan tetap di ruang atau bergerak bersama dengan fluida

Setiap turunan umumnya dimulai dengan integral definit dari suatu jumlah, misalnya 𝜳, atas volume V yang diformulasikan dengan persamaan.

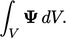(2.1)

Jika notasi di atas tidak familiar, pahami bahwa maksud dari penjelasan di atas berupa penjumlahan untuk semua penambahan volume dV yang membentuk total volume V. Nilai-nilai yang dijumlahkan adalah (𝜳 x dV), dimana 𝜳 adalah nilai pada dV yang bersangkutan

Turunan-turunan juga menggunakan integral permukaan S, misalnya

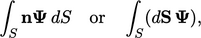(2.2)

Dimana dS = ndS. Integral volume dan permukaan terhubung melalui Theorema Gauss.