16.4 Diskritisasi Persamaan Momentum
Diskritisasi persamaan momentum. Persamaan momentum yang terdiskritisasi, Eq. (16.2), di atas volume kontrol C yang ditunjukkan dalam Gambar 16.1 mirip dengan bentuknya yang tidak dapat dipadatkan yang diberikan di Bab 15. Hanya ada dua perbedaan terkait dengan interpolasi kepadatan ke antarmuka dan istilah tambahan yang melibatkan viskositas bulk. Mulai dengan perbedaan pertama, kepadatan dalam aliran dapat dipadatkan tidak lagi konstan dan karena disimpan di pusat volume kontrol, itu harus diinterpolasi untuk menemukan nilainya di wajah volume kontrol di mana dibutuhkan untuk menghitung laju aliran massa. Penggunaan profil interpolasi linear (perbedaan pusat) menyebabkan osilasi pada kecepatan tinggi. Oleh karena itu, skema berbatas dengan kecenderungan upwind harus digunakan. Salah satu dari skema konvektif yang berbatas yang disajikan di Bab 11 dan 12 dapat diadopsi untuk tujuan tersebut. Perbedaan kedua adalah istilah tambahan yang melibatkan
Istilah ini belum terdiskritisasi sejauh ini dan bentuk terdiskritisasinya diperoleh dengan menggunakan Persamaan (2.85) berdasarkan integral volume dari gradien suatu jumlah skalar adalah

Gambar 16.1 gambar skematik dari volume kontrol C beserta tetangganya.
ditransformasikan menjadi integral permukaan dan kemudian menjadi penjumlahan fluks di atas wajah-wajah volume kontrol sesuai dengan
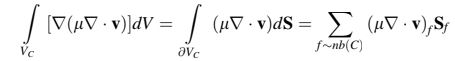
Divergensi dari vektor kecepatan di wajah-wajah dihitung sebagai

di mana gradien dari atau
diinterpolasi secara linear ke wajah
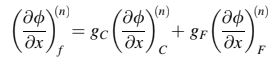
Bentuk terdiskritisasi akhir dari persamaan momentum diberikan oleh Persamaan (15.70) dengan koefisien-koefisiennya diberikan oleh Persamaan (15.71) dengan istilah
Ditambahkan ke suku sumber dalam persamaan tersebut. Seperti pada masalah aliran tidak dapat dipadatkan, persamaan aljabarik di-relaksasi dan ditulis dalam bentuk Persamaan (15.78), yang sesuai untuk penurunan persamaan koreksi tekanan.
