Domain discretization

Domain Discretization. Model matematika menggunakan variabel kontinu. Transisi dari representasi kontinu aliran dengan medan kontinu yang mengisi domain aliran Ω, ke domain terdiskritisasi ΩD ditunjukkan dalam gambar 1.1.

dimana gabungan ΩD adalah mesh volume terbatas dan C adalah himpunan yang berisi indeks dari semua sel dalam mesh ΩD. Setiap volume terbatas menyimpan nilai rata-rata volume dari properti fisik (misalnya suhu) yang terkait dengan pusat beratnya xc. Mari kita asumsikan bahwa medan φ dapat direpresentasikan menggunakan ekspansi deret Taylor sebagai berikut:

Nilai rata-rata volume dari φ(x) di dalam sel Ωc dengan ekspansi deret Taylor dalam (1.3) memperkenalkan jumlah yang didefinisikan pada titik xc, yang konstan di seluruh Ωc.

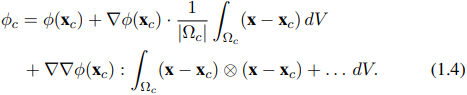
Definisi dari pusat berat xc dari volume Ωc menghasilkan persamaan

yang dimasukkan ke dalam persamaan (1.4) menghasilkan persamaan

Persamaan (1.6) menunjukkan bahwa nilai rata-rata dari φ di atas volume terbatas Ωc sama persis dengan nilai φ di pusat berat xc dari Ωc untuk φ linear, karena untuk φ linear turunan orde tinggi adalah nol.

INFO
Diskritisasi domain dari FVM tak terstruktur yang memberikan nilai rata-rata sel φc dari φ di centroid dari sel adalah akurat hingga orde kedua.

Sebuah interpolasi dari φ berdasarkan pada (1.6),

berorde kedua, karena suku terbesar dalam bagian yang dipotong dari deret Taylor dalam persamaan (1.6) berskala dengan

Pada persamaan (1.3), gradien ∇φ(xc) di pusat sel juga harus didekati. Sebelum memahami bagaimana persamaan didiskritisasi, mesh ΩD harus didefinisikan secara lebih rinci, khususnya bagaimana sel {Ωc}c∈C terhubung satu sama lain.

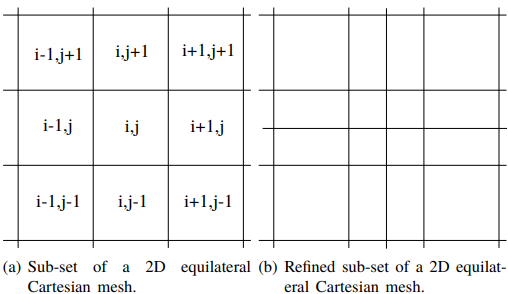
Gambar 1.2: mesh kuadratik terstruktur.

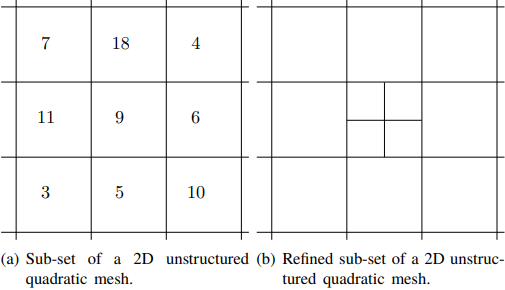
Gambar 1.3: mesh kuadratik tidak terstruktur.

Mesh domain discretization secara terstruktur meningkatkan akurasi absolut interpolasi yang terlibat dalam FVM, tetapi membuat mesh kurang fleksibel saat digunakan untuk pembuatan mesh pada domain geometri yang kompleks.

Gambar 1.4: Distribusi kualitatif densitas ρ terhadap ketinggian h di atas permukaan bebas.

INFO
Meskipun konektivitas mesh dalam OpenFOAM sepenuhnya tidak terstruktur, seringkali mesh akan dibentuk secara blok demi blok untuk kasus-kasus dengan geometri domain sederhana (utilitas blockMesh): ini tidak berarti bahwa mesh terstruktur blok dibuat.

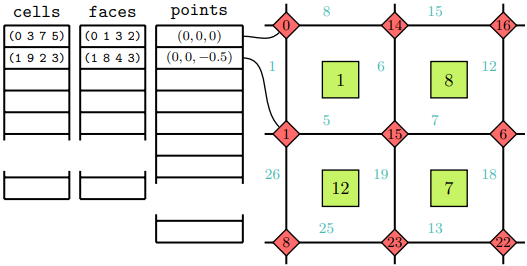
Gambar 1.5: Contoh konektivitas mesh tak terstruktur 2D dengan label berbagai bentuk yang digunakan untuk sel (persegi), titik (wajik), dan permukaan.

Cara elemen-elemen mesh diakses oleh algoritma metode numerik ditentukan oleh konektivitas mesh. OpenFOAM mengandalkan addressing tidak langsung, owner-neighbor addressing, dan boundary mesh addressing untuk mengakses elemen-elemen mesh.

Owner-neighbor addressing
Metode ini menentukan sel mana yang memiliki suatu surface tertentu dan tetangganya. Selain itu, ini merupakan optimasi akses ke surface-surface mesh.

Addressing tidak langsung
Metode ini mendefinisikan bagaimana mesh disusun dari titik-titik mesh, yang diberikan sebagai daftar global dari titik-titik. Surface sel diindeks oleh daftar titik mesh global menggunakan label bilangan bulat.

Boundary addressing
Metode ini mengurus bagaimana surface-surface di tepi diberi alamat. Secara definisi, semua surface yang hanya memiliki satu sel pemilik dan tidak ada sel tetangga, adalah surface tepi.

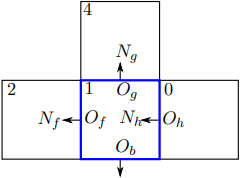
Gambar 1.6: Penyandian pemilik-tetangga untuk sebuah sel contoh (bingkai biru) dengan label sel 1, label surface internal f, g, h, dan label surface batas b.