Efek Kompresibilitas
Salah satu asumsi utama adalah bahwa fluida tidak dapat dimampatkan. Meskipun ini masuk akal untuk sebagian besar aliran cairan, dalam beberapa kasus, ini dapat memperkenalkan kesalahan yang considerable untuk gas.
Pada bagian sebelumnya, kita melihat bahwa tekanan stagnasi, p stag , lebih besar dari tekanan statis, p static , sebesar static Δp=p stag −p static= ρV2/2 , asalkan densitas tetap. Jika tekanan dinamis ini tidak terlalu besar dibandingkan dengan tekanan statis, perubahan densitas antara dua titik tidak terlalu besar dan aliran dapat dianggap tidak dapat dimampatkan. Namun, karena tekanan dinamis bervariasi sebagai V2, kesalahan yang terkait dengan asumsi bahwa fluida tidak dapat dimampatkan meningkat dengan kuadrat kecepatan fluida, seperti yang ditunjukkan dalam gambar di pinggir. Untuk memperhitungkan efek kompresibilitas, kita harus kembali ke Persamaan 3.6 dan mengintegrasikan dengan benar term ∫ dp/p ketika ρ tidak konstan.
Kasus sederhana, meskipun spesialis, dari aliran dapat dimampatkan terjadi ketika suhu gas sempurna tetap konstan sepanjang garis aliran — aliran isotermal. Dengan demikian, kita mempertimbangkan p=ρRT, di mana T konstan. Secara umum, ρ, p dan T akan bervariasi. Untuk aliran steady, tak kental, isotermal, Persamaan 3.6 menjadi
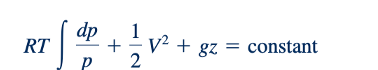
di mana kita telah menggunakan ρ= p /RT . Istilah tekanan mudah diintegrasikan dan konstanta integrasi dievaluasi jika z1,p1, dan V1 diketahui di suatu lokasi pada garis aliran. Hasilnya adalah
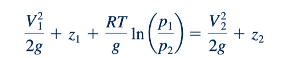
Persamaan 3.23 adalah analogi isotermal, tak kental dari persamaan Bernoulli yang tidak dapat dimampatkan. Pada batas perbedaan tekanan yang kecil, p1/p2 = 1+ (p1-p2) /p2 = 1+ 𝜀, dengan 𝜀 < 1, dan Persamaan 3.23 mengurangi persamaan Bernoulli tak dapat dimampatkan standar. Ini dapat ditunjukkan dengan menggunakan aproksimasi (1+𝜀)≈𝜀 untuk nilai 𝜀 yang kecil. Penggunaan Persamaan 3.23 dalam aplikasi praktis dibatasi oleh asumsi aliran tak kental, karena seperti yang dibahas di Bagian 11.52, sebagian besar aliran isotermal disertai dengan efek viscous.
Kondisi aliran kompresibel yang jauh lebih umum adalah aliran isentropik (konstan entropi) dari gas sempurna. Aliran seperti ini adalah proses adiabatik reversibel — "tidak ada gesekan atau perpindahan panas" — dan mendekati dalam banyak situasi fisik. Seperti yang dibahas secara lengkap di Bab 11, untuk aliran isentropik dari gas sempurna, densitas dan tekanan terkait oleh p=ρ /k=C, di mana k adalah rasio panas spesifik dan C adalah konstanta. Oleh karena itu, integral ∫ dp/p dari Persamaan 3.6 dapat dievaluasi sebagai berikut. Densitas dapat ditulis dalam hal tekanan sebagai ρ=k1/k C1/k, sehingga Persamaan 3.6 menjadi
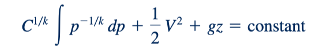
Istilah tekanan dapat diintegrasikan antara titik (1) dan (2) pada garis aliran dan konstanta C dievaluasi di salah satu titik (baik C1/k = p1(1/k) /p1 atau C 1/2(1/k) /p2 ) untuk memberikan yang berikut:
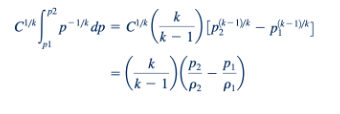
Oleh karena itu, bentuk akhir dari Persamaan 3.6 untuk aliran isentropik, stabil, dan kompresibel dari gas sempurna adalah:
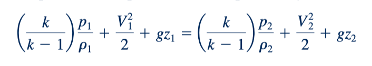
Kesamaan antara hasil untuk aliran isentropik kompresibel (Persamaan 3.24) dan aliran isentropik tak dapat dimampatkan (persamaan Bernoulli, Persamaan 3.72) jelas terlihat. Satu-satunya perbedaan adalah faktor [𝑘/(𝑘−1)] yang mengalikan istilah tekanan dan kenyataan bahwa densitasnya berbeda (ρ1 ≠ ρ2). Dalam batas "aliran kecepatan rendah", kedua hasil tersebut sama persis, seperti yang terlihat dari yang berikut ini.
Kita pertimbangkan aliran titik stagnasi dari Bagian 3.5 untuk mengilustrasikan perbedaan antara hasil tak dapat dimampatkan dan hasil kompresibel. Seperti yang ditunjukkan dalam Bab 11, Persamaan 3.24 dapat dituliskan dalam bentuk tak berdimensi sebagai:
di mana (1) menunjukkan kondisi hulu dan (2) kondisi stagnasi. Kami telah mengasumsikan z1= z2, V2 =0, dan telah menunjukkan Ma1= c1/V1 sebagai bilangan Mach hulu — rasio kecepatan fluida terhadap kecepatan suara, c1 √𝑘𝑅𝑇1 .
Perbandingan antara hasil kompresibel dan hasil tak dapat dimampatkan mungkin paling mudah dilihat jika kita menulis hasil aliran tak dapat dimampatkan dalam bentuk rasio tekanan dan bilangan Mach. Dengan demikian, kita membagi setiap istilah dalam persamaan Bernoulli, konstan ρV1,2 / 2 + p1= p2, oleh p1 dan menggunakan hukum gas sempurna pada titik (1), p1=ρRT1, untuk mendapatkan:
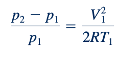
karena Ma1 = V1 √𝑘𝑅𝑇1 ini dapat ditulis sebagai :
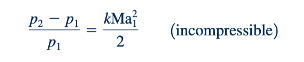
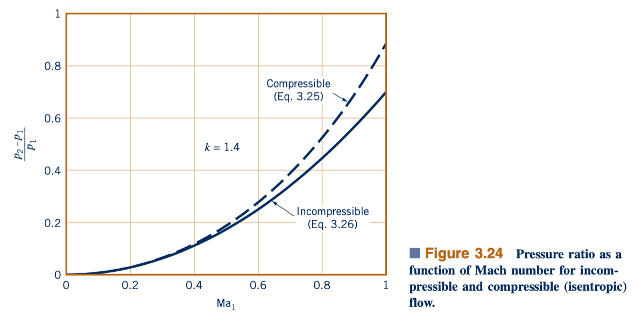
Persamaan 3.25 dan 3.26 digambarkan dalam Gambar 3.24. Pada batas kecepatan rendah dari Ma≤0, kedua hasilnya sama. Ini dapat dilihat dengan menunjukkan (k-1) Ma 2,1/2 = 𝜀 dan menggunakan ekspansi binomial, (1+ 𝜀)n = 1+ n𝜀 + n(n-1)𝜀2/2+ . . . .dimana n = k/(k-1), untuk menuliskan Persamaan 3.25 sebagai:
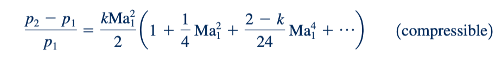
Untuk Ma 1 ≈ 1, hasil aliran kompresibel ini setuju dengan Persamaan 3.26. Persamaan tak dapat dimampatkan dan kompresibel setuju hingga sekitar 2% sampai dengan bilangan Mach sekitar Ma 1 ≈ 0.3. Untuk bilangan Mach yang lebih besar, ketidaksepakatan antara kedua hasil tersebut meningkat.
Dengan demikian, suatu aturan praktis adalah bahwa aliran gas sempurna dapat dianggap tidak dapat dimampatkan selama bilangan Mach kurang dari sekitar 0.3. Pada udara standar (T1 = 59°F c1 = √𝑘𝑅𝑇1= 1117 ft/s), ini setara dengan kecepatan V1 =Ma1. C1 = 0.3(1117ft/s )≈ 335ft/s ≈ 228mi/hr. Pada kecepatan yang lebih tinggi, kompresibilitas mungkin menjadi penting.

