Efek Tak Stabil
Keterbatasan lain dari persamaan Bernoulli (Persamaan 3.72) adalah asumsi bahwa aliran adalah steady. Untuk aliran semacam itu, pada sebuah garis aliran yang diberikan, kecepatan adalah fungsi hanya dari s, lokasi sepanjang garis aliran tersebut. Artinya, sepanjang garis aliran V=V(s). Untuk aliran yang tidak steady, kecepatan juga merupakan fungsi dari waktu, sehingga sepanjang garis aliran V=V(s,t). Jadi, ketika mengambil turunan waktu dari kecepatan untuk mendapatkan percepatan sepanjang aliran, kita mendapatkan as = ∂t/∂V+ ∂s/∂V dari pada hanya as= V ∂v/∂s seperti yang benar untuk aliran steady. Untuk aliran steady, percepatan disebabkan oleh perubahan kecepatan akibat perubahan posisi partikel (term V ∂V/∂s), sedangkan untuk aliran tidak steady ada kontribusi tambahan terhadap percepatan yang disebabkan oleh perubahan kecepatan terhadap waktu pada lokasi tetap (term ∂V/∂t ). Efek-efek ini dibahas secara detail di Bab 4. Efek bersihnya adalah bahwa penambahan term tidak steady, ∂V/∂t , tidak memungkinkan persamaan gerak untuk diintegrasikan dengan mudah (seperti yang dilakukan untuk mendapatkan persamaan Bernoulli) kecuali asumsi tambahan dibuat.
Persamaan Bernoulli diperoleh dengan mengintegrasikan komponen hukum kedua Newton (Persamaan 3.52) sepanjang garis aliran. Ketika diintegrasikan, kontribusi percepatan dalam persamaan ini, yaitu istilah 1/2 pd(V2), menghasilkan istilah energi kinetik dalam Persamaan Bernoulli. Jika langkah-langkah yang mengarah kepada ini
saat persamaan 3.5 diulang dengan inklusi efek tidak stabil (∂t/∂V =0) , yang berikut ini diperoleh:
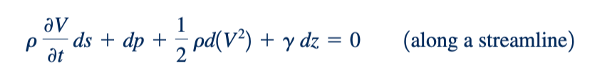
Untuk aliran tak dapat dimampatkan ini dapat dengan mudah diintegrasikan antara titik (1)dan (2) untuk memberikan
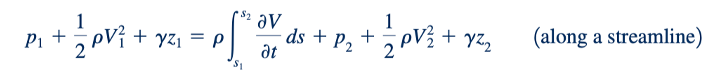
Persamaan 3.27 adalah bentuk tak stabil dari persamaan Bernoulli yang valid untuk aliran tak stabil, tak dapat dimampatkan, tak kental. Kecuali untuk integral yang melibatkan percepatan lokal, ∂t/∂V , persamaan ini identik dengan persamaan Bernoulli stabil. Secara umum, tidak mudah untuk mengevaluasi integral ini karena variasi ∂t/∂V sepanjang garis aliran tidak diketahui. Dalam beberapa situasi, konsep "aliran tanpa putaran" dan "potensial kecepatan" dapat digunakan untuk menyederhanakan integral ini. Topik-topik ini dibahas di Bab 6.

Dalam beberapa kasus aliran tidak stabil, aliran dapat dibuat menjadi stabil dengan pemilihan sistem koordinat yang sesuai. Contoh 3.17 mengilustrasikan hal ini.

