Equation discretization

Persamaan discretization

Equation discretization. Setelah domain di-discretize menjadi volume terbatas, aproksimasi diterapkan pada istilah-istilah dalam model matematika yang mengubah operator diferensial (∂t, ∇, ∇·)

Ingatlah rata-rata volume yang akurat hingga orde kedua yang terkait dengan centroid Ωc yang diberikan oleh

Term temporal dari persamaan (1.8) menggunakan notasi singkat f(xc) = fc untuk nilai berpusat sel,

Term temporal ∂tφc kemudian dapat diaproksimasi menggunakan finite differences.

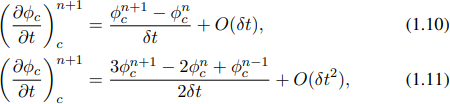
di mana n + 1 adalah langkah waktu baru, n adalah langkah waktu saat ini, dan n – 1 adalah langkah waktu sebelumnya

Persamaan (1.8) juga memuat istilah divergensi (adveksi) ∇·(Uφ), yang didiskretisasi menggunakan teorema divergensi:

Batas ∂Ωc dari Ωc, yang digunakan pada r.h.s, merupakan gabungan permukaan (surface) yang dibatasi oleh segmen garis (sisi), yaitu

di mana Fc adalah himpunan indeks dari wajah Sf dari sel Ωc, dan integral di r.h.s. persamaan (1.13) dapat ditulis sebagai

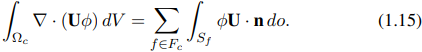
Gambar 1.7: Contoh sel dodekahedron: dodekahedron cembung, dodekahedron tidak cembung dengan surface non-planar, dodekahedron tidak cembung dengan wajah non-cembung planar.

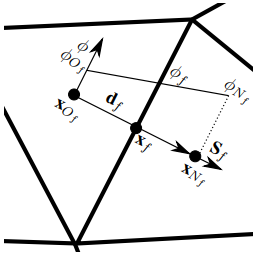
Untuk lebih mendiskritisasi persamaan (1.15), perataan dari $ϕ$ dilakukan untuk setiap wajah $S_{f}$ , di $x_{f}$ , sentroid dari wajah $S_{f}$ , yaitu:

dimana $ϕ_{f} = ϕ (x_{f})$ . Memasukkan persamaan (1.16) ke dalam persamaan (1.15) menghasilkan:

Diskretisasi spasial yang akurat hingga orde kedua dari suatu suku divergensi diberikan oleh persamaan (1.1).

Gambar 1.8: Skema interpolasi beda pusat yang diterapkan pada jaringan segitiga ortogonal

Jika nilai titik pusat muka φf dinyatakan menggunakan interpolasi linier (Central Differencing Scheme (CDS)), kita mempunyai

dimana

adalah koefisien delta yang disebut dalam OpenFOAM, dan wf yang dihitung dengan skema CDS adalah koefisien wajah linier

Koefisien wajah wf ∈ [0, 1] dapat dihitung dengan cara yang berbeda. berikut perhitungan wf :

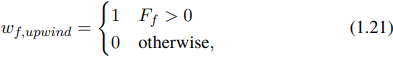
di mana Ff adalah fluks volumetrik skalar di xf.

Menghitung rata-rata berpusat pada wajah sebagai kombinasi dari nilai berpusat sel dari sel tetangga, menghasilkan operator divergensi diskrit $\nabla_{c} \cdot (\cdot)$

di mana $F_{c}$ adalah himpunan indeks dari semua wajah yang termasuk dalam sel $Ω_{c}$ .

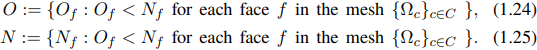
Set indeks $O$ dan $N$ yang diberikan oleh persamaan (1.24) dan (1.25) mengandung label masing-masing sel pemilik dan tetangga untuk setiap wajah dalam mesh, bukan untuk setiap wajah dari sel seperti yang dilakukan oleh set indeks $F_{c}$ dalam persamaan (1.23).

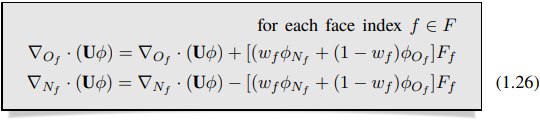
di mana F adalah himpunan indeks dari semua wajah dalam mesh, $O_{f}$ adalah indeks dari sel pemilik wajah dari $O$ yang diberikan oleh persamaan (1.24), $N_{f}$ adalah indeks dari sel tetangga wajah $N$ yang diberikan oleh persamaan (1.25), dan $\nabla \cdot$ adalah operator divergensi diskrit yang diberikan oleh persamaan (1.23).

di persamaan (1.26).

Suku Laplace (difusi) dari persamaan (1.1) didiskretisasikan dengan cara yang sama seperti suku divergensi (adveksi). Discretisasi dimulai dengan integral atas $Ω_{c}$ dan penerapan teorema divergensi, menggunakan notasi singkat $Γ_{f} := Γ (x_{f})$ , $\nabla ϕ (x_{f}) := (\nabla ϕ)_{f}$ , yang menghasilkan:

Untuk nilai berpusat pada wajah, xOf −xf := xf xOf dan φOf:= φ(xOf) digunakan (sama dengan Nf, f), ditambah dengan notasi untuk hasil perkalian tensor dari sebuah vektor a:

Dengan menggunakan notasi ini, deret Taylor dari pusat wajah, pemilik wajah, dan tetangga secara berturut-turut diberikan sebagai:

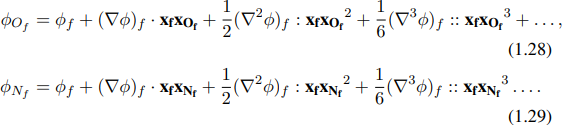
Pengurangan persamaan (1.28) dari persamaan (1.29), menghasilkan:

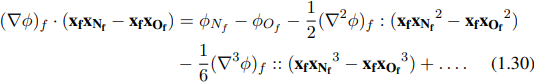
Pada jaringan yang berjarak sama, mirip dengan jaringan yang ditunjukkan dalam gambar 1.8, pusat wajah xf membagi vektor df = xNf − xOf menjadi dua bagian yang sama besar, sehingga:

Memasukkan persamaan (1.31) ke dalam persamaan (1.30), mengalikan hasilnya dengan ·df , dan membaginya dengan

membatalkan suku orde kedua dalam persamaan (1.30), yaitu:

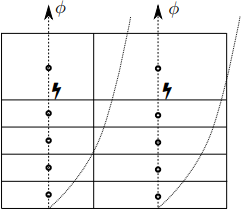
Gambar 1.9: Kerugian dalam akurasi dari diskritisasi gradien dalam lapisan batas, disebabkan oleh rasio aspek yang berbeda dari 0,5 untuk wajah dengan perubahan kuat dalam φ, dalam arah vertikal.

yang menghasilkan diskritisasi akhir dari gradien berpusat pada wajah sebagai

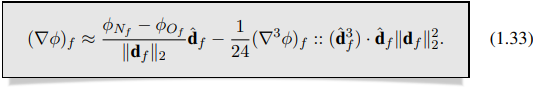
Persamaan (1.33) menunjukkan akurasi orde kedua dari gradien berpusat pada wajah dalam hal

Namun, hanya pada jaringan yang sama jaraknya yang memenuhi persamaan (1.31), dan untuk φ yang cukup teratur yang dapat diperluas menjadi deret Taylor.

dari persamaan (1.30), yang membuat diskritisasi menjadi akurat tingkat pertama.

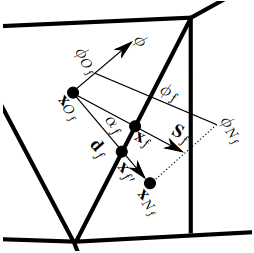
Gambar 1.10: Sebuah mesh 2D non-ortogonal.

Dengan diskritisasi yang akurat hingga orde kedua dari (∇φ)f, diskritisasi dari suku Laplace diselesaikan dengan memasukkan persamaan (1.33), yang menghasilkan diskritisasi FVM yang akurat hingga orde kedua dari suku Laplace (difusi)

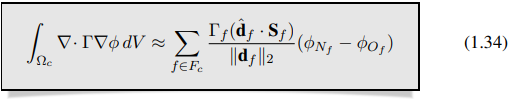
Diskritisasi suku Laplace oleh persamaan (1.34) dapat lebih disederhanakan jika dˆf dan Sˆf sejajar (dˆf · Sˆf = 1), atau dengan kata lain, jika mesh bersifat ortogonal, seperti

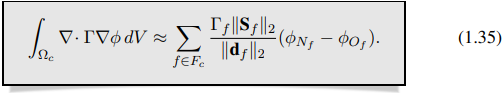
Sebuah mesh nonortogonal ditampilkan dalam gambar 1.10: dalam mesh nonortogonal, pada face Sf, vektor (dˆf, Sˆf) tidak sejajar dan membentuk sebuah sudut nonortogonalitas yang disebut sudut nonortogonalitas αf :=∡(dˆf, Sˆf).

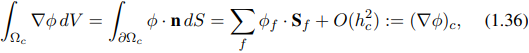
Jika persamaan (1.36) diinterpolasi secara linier dengan persamaan (1.18) pada centroid face, yaitu

Gradien berpusat pada face tetap mempertahankan akurasi tingkat kedua dari gradien pada owner dan tetangga yang diberikan oleh persamaan (1.36), karena interpolasi linier dibatasi, yang berarti ia mempertahankan batas kesalahan O(h^2) dari sel Nf dan Of.

Papan catur adalah ketidakmampuan diskritisasi untuk menghitung (∇φ)c karena pembatalan buatan yang hadir dalam persamaan (1.37) untuk beberapa kasus. ,

Tiga pendekatan biasanya digunakan untuk dekomposisi vektor normal area permukaan: koreksi minimum, koreksi ortogonal, dan koreksi terlebih santai (lihat [3, bagian 3.3.1.3], [5, bagian 3.3.2], [6, bagian 8.6]). Ketiga pendekatan tersebut mendekomposisi vektor normal area permukaan menjadi bagian ortogonal yang sejajar dengan dan bagian tidak ortogonal , yaitu

sehingga

Berbagai pendekatan untuk menghitung ditunjukkan dalam gambar 1.11 dan dihitung dari persamaan (1.39). Kontribusi ortogonal terhadap gradien dalam persamaan (1.40), , dievaluasi menggunakan persamaan (1.33), yang melibatkan dua rata-rata sel yang berdekatan dengan wajah dan diskritisasi secara implisit. Kontribusi nonortogonal diskritisasi secara eksplisit.

Gambar 1.11: Koreksi Nonortogonalitas.

Diskritisasi eksplisit dari dalam persamaan (1.40) menghasilkan

Untuk memperbaiki ketidaksesuaian antara dan dalam persamaan (1.40), koreksi nonortogonal dalam OpenFOAM dilakukan dengan melakukan jumlah iterasi tambahan yang tetap M dalam setiap langkah waktu, yaitu

dengan harapan bahwa setelah M iterasi . Itulah mengapa file konfigurasi untuk algoritma kopling tekanan-kecepatan dalam OpenFOAM memiliki entri yang sesuai.

Diskritisasi temporal menggabungkan diskritisasi suku temporal, konveksi (divergensi), dan difusi (Laplace) yang telah dijelaskan sejauh ini:

Membangun φc dalam waktu menggunakan deret Taylor, dengan sebagai langkah waktu, memberikan

dan

Memasukkan persamaan (1.46) ke dalam persamaan (1.42) menghasilkan diskritisasi persamaan transpor skalar (1.1) dengan skema Euler implisit yang sering digunakan yaitu akurasi orde pertama dalam waktu dan akurasi orde kedua dalam ruang:

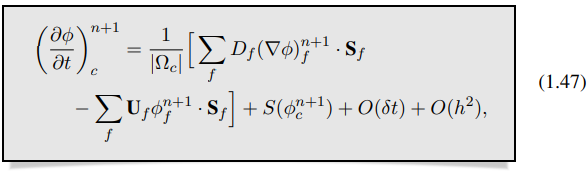
di mana term sumber dievaluasi pada langkah waktu lama , atau diekstrapolasi dalam φ dan waktu menggunakan linearisasi. Informasi tambahan tentang linearisasi term sumber dapat ditemukan di [7].

ini juga akurat dalam waktu orde kedua, karena suku dan saling meniadakan dalam penjumlahan persamaan (1.44) dan persamaan (1.46), sehingga menyisakan sebagai istilah pemotongan terkemukan.

mengelompokkan bersama-sama istilah implisit dan eksplisit, yaitu

Ketika , persamaan (1.48) dipulihkan dari persamaan (1.49). Jika persamaan (1.46) digunakan untuk , menghasilkan metode implisit Euler orde pertama yang diberikan oleh persamaan (1.47).

Sebuah sistem persamaan aljabar linear dibangun oleh diskritisasi persamaan, dipecahkan untuk di setiap sel Ωc dari mesh ΩD. Istilah-istilah dan , dari langkah-langkah waktu n, n + 1. Istilah-istilah lain, seperti hanya mengandung nilai-nilai φc dari langkah waktu n saat ini dan langkah waktu baru n+ 1.

Gambar 1.12: Contoh aliran saluran 2D sederhana dengan aliran masuk di sisi kanan dan aliran keluar di sisi kiri. Dua batas lainnya diasumsikan sebagai dinding.

Kondisi batas Neumann, atau dikenal sebagai “kondisi batas alami”, mengatur gradien nol dari sifat di batas domain:

Ini adalah kondisi yang digunakan untuk menghitung nilai sifat di wajah batas b, menggunakan pendekatan deret Taylor:

jadi nilai di wajah batas mengambil nilai dari pusat sel untuk kondisi batas nol gradien, yaitu

Menyelesaikan sistem persamaan aljabar linear (sistem linier) yang dihasilkan oleh FVM tidak berstruktur sering memerlukan upaya komputasi yang substansial, karena ukurannya adalah , di mana adalah jumlah sel dalam mesh ΩD dan d adalah dimensi spasial. Koefisien di sebelah dalam persamaan (1.50) oleh karena itu merupakan koefisien dalam matriks sparse besar .