Error Sources
Error sources. Berdasarkan diskusi dalam bagian-bagian sebelumnya, sumber kesalahan numerik dalam diskritisasi fluks konvektif dapat dibagi menjadi difusi numerik dan dispersi numerik. Difusi numerik, yang menyebabkan penyamaran gradien tajam (Gambar 11.18a), juga dapat dibagi menjadi difusi numerik sepanjang arus dan lintas arus. Difusi numerik sepanjang arus dapat dikurangi dengan meningkatkan urutan profil interpolasi, seperti yang ditunjukkan dalam Gambar 11.18b, menghasilkan profil yang lebih tajam tetapi memunculkan under/overshoots dalam keberadaan gradien besar. Difusi numerik lintas arus, yang ditunjukkan dalam Gambar 11.17b, disebabkan oleh sifat satu dimensi dari profil yang diasumsikan dan dapat dikurangi baik dengan interpolasi dalam arah aliran (yaitu, profil multi-dimensi) [15, 16] atau dengan menggunakan profil interpolasi satu dimensi yang lebih tinggi (Gambar 11.18b). Kesalahan dispersi numerik muncul melalui osilasi dalam profil yang dihasilkan dalam keberadaan gradien besar yang membuat solusi tidak terbatas. Seperti yang ditunjukkan dalam Gambar 11.18b dan 11.19 serta hasil yang dilaporkan dalam Gambar 11.14b, itu ada dengan semua profil interpolasi yang diasumsikan kecuali skema upwind. Ini adalah hasil dari perilaku tidak fisik dari profil interpolasi yang diasumsikan.
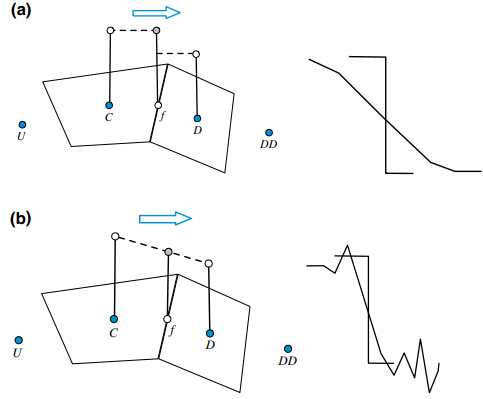
Gambar 11.18 a Penyamaran profil tajam oleh difusi numerik dan b wiggles dalam profil yang dihitung akibat dispersi numerik

Gambar 11.19 Kesalahan dispersi numerik yang menyebabkan osilasi dalam keberadaan gradien besar
Suatu evaluasi dari kesalahan ini dapat diperoleh dengan menggunakan versi sederhana dari Persamaan (11.73) di mana difusi dan sumber diabaikan. Jika selanjutnya, medan kecepatan dan kepadatan dianggap konstan, Persamaan (11.73) disederhanakan menjadi

Dengan asumsi solusi eksak berbentuk
Dimana j adalah bilangan imajiner yang didefinisikan oleh j2=−1. Maka nilai eksak gradiennya adalah:
Dengan profil interpolasi, pendekatan numerik dari gradien ditulis dalam istilah nilai ϕ pada lokasi -MΔx, (-M+1)Δx, …, Δx, 2Δx, …, NΔx sebagai

yang setelah substitusi solusi yang diasumsikan, menjadi:

Dengan membandingkan solusi eksak dan numerik, didapatkan bahwa:
Secara umum, k adalah bilangan imajiner yang dapat dituliskan sebagai:
di mana Re dan Im merujuk pada bagian real dan imajiner, masing-masing. Memasukkan k dalam solusi eksak, solusi perkiraan diperoleh sebagai:

Oleh karena itu, solusi numerik mungkin termasuk kedua kesalahan difusi (atau redaman) dan dispersi. Jika k adalah bilangan real, hanya kesalahan dispersi yang terjadi. Namun jika k adalah kompleks, maka kedua jenis kesalahan akan muncul. Berdasarkan analisis ini, nilai k untuk skema upwind dan CD dapat diperiksa. Untuk skema upwind, gradien dihitung sebagai:

Jelas bahwa skema upwind menimbulkan kedua jenis kesalahan. Untuk skema perbedaan sentral, gradiennya diberikan oleh:

Sejak k bersifat imajiner, maka hanya kesalahan dispersi numerik yang muncul. Kesalahan dispersi ini menyebabkan osilasi dan under/overshoots dalam solusi. Setelah memperoleh pemahaman yang lebih baik tentang dispersi numerik, sangat diinginkan untuk mengembangkan skema konvektif non-osilatori dengan tingkat akurasi tinggi. Hal ini telah membuat para peneliti sibuk untuk periode waktu yang cukup lama hingga pembatasan aliran konvektif menjadi dipahami. Pengembangan skema semacam itu akan diuraikan dalam bab berikutnya.
