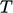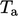4.17 External wall heat Flux

External wall heat flux. Kondisi batas suhu (atau energi) menentukan perpindahan panas melintasi suatu batas. Pada batas yang mewakili dinding kokoh, kondisi sederhana terkadang dapat diterapkan. Namun, kondisi batas khusus seringkali diperlukan untuk mengendalikan fluks panas melintasi batas.

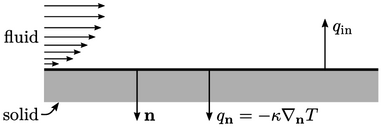
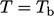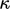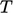Suhu tetap adalah kondisi paling sederhana, menetapkan nilai tetap $persamaan$ . Kondisi ini memberikan perkiraan untuk kasus benda padat dengan massa termal tinggi ,karena massa material yang besar dan konduktivitas yang tinggi $persamaan$ , yang membantu menjaga konstan $persamaan$ .

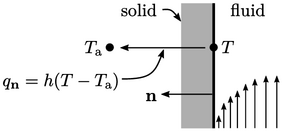
Jika tidak, kondisi batas menetapkan fluks panas normal terhadap batas, 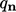$persamaan$ yang diturunkan dari Persamaan. (2.54) oleh

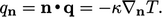qn = n q = rnT: \relax \special {t4ht=

(4.28)

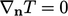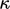Kondisi sederhana lainnya adalah gradien nol $persamaan$ . Ini adalah kondisi adiabatik ,sesuai dengan fluks panas normal nol dengan Persamaan. (4.28), cocok jika padatan tersebut merupakan bahan isolasi termal dengan massa besar dan rendah $persamaan$ .

Jika tidak, fluks panas tetapkondisi menentukan fluks panas ke dalam 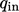$persamaan$ sebagai tipe gradien tetap dengan gradien referensi sebesar

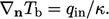r T = q = : n b in \relax \special {t4ht=

(4.29)

Koefisien perpindahan panas tetap

Cara lain untuk menentukan perpindahan panas pada dinding luar adalah dengan hukum pendinginan Newton.Hukum umum ini menyatakan laju kehilangan panas suatu benda berbanding lurus dengan perbedaan antara suhu tubuh $persamaan$ dan suhu lingkungan sekitar $persamaan$ .

Yang diterapkan sebagai syarat batas 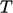$persamaan$ adalah suhu fluida pada batas tersebut, dan 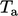$persamaan$ suhu pada jarak tertentu di luar batas padat. Koefisien perpindahan panas 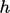$persamaan$ , dengan satuan SI 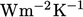$persamaan$ , memberikan konstanta proporsionalitas sedemikian rupa

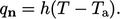qn = h(T Ta): \relax \special {t4ht=

Mengganti Persamaan. (4.28) dan penataan ulang memberikan persamaan untuk kondisi koefisien perpindahan panas tetap :

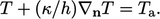T + ( =h)rnT = Ta: \relax \special {t4ht=

(4.31)

Persamaannya berbentuk kondisi Robin, Persamaan. (4.10), sehingga dapat diimplementasikan seperti yang dijelaskan dalam Bagian. 4.9. Koefisien ini 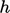$persamaan$ biasanya dikarakterisasi untuk rezim aliran tertentu dan batas padat, dengan beberapa perkiraan, pengukuran eksperimental atau simulasi komputer.