Fungsi Aliran
Fungsi Aliran. Aliran mantap, tidak dapat dimampatkan, bidang, dua dimensi mewakili salah satu jenis aliran yang paling sederhana yang penting secara praktis. Dengan "bidang, aliran dua dimensi" kami maksudkan bahwa hanya ada dua komponen kecepatan, seperti u dan v, ketika aliran dianggap berada dalam bidang x–y. Untuk aliran ini, persamaan kontinuitas, Persamaan 6.31, menyederhanakan menjadi
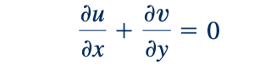
Kita masih memiliki dua variabel, u dan v, yang harus diatasi, tetapi mereka harus saling terkait dengan cara khusus seperti yang diindikasikan oleh Persamaan 6.36. Persamaan ini menyarankan bahwa jika kita mendefinisikan fungsi 𝜓 (x, y), yang disebut fungsi aliran, yang menghubungkan kecepatan seperti yang ditunjukkan oleh gambar di pinggir sebagai

maka persamaan kontinuitas terpenuhi secara identik. Kesimpulan ini dapat diverifikasi dengan hanya menggantikan ekspresi untuk u dan v ke dalam Persamaan 6.36 sehingga


Dengan demikian, setiap kali komponen kecepatan didefinisikan dalam hal fungsi aliran, kita tahu bahwa konservasi massa akan terpenuhi. Tentu saja, kita masih tidak tahu apa itu 𝜓(x, y) untuk masalah tertentu, tetapi setidaknya kita telah menyederhanakan analisis dengan hanya harus menentukan satu fungsi yang tidak diketahui, yaitu 𝜓(x, y), daripada dua fungsi, u(x, y) dan v(x, y).
Salah satu keuntungan khusus lain dari menggunakan fungsi aliran terkait dengan fakta bahwa garis-garis di mana c konstan adalah garis aliran. Ingat dari Bagian 4.1.4 bahwa garis aliran adalah garis dalam medan aliran yang di mana pun bersinggungan dengan kecepatan, seperti yang diilustrasikan dalam Gambar 6.7. Dari definisi garis aliran, dapat disimpulkan bahwa kemiringan di setiap titik sepanjang garis aliran diberikan oleh
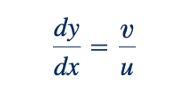
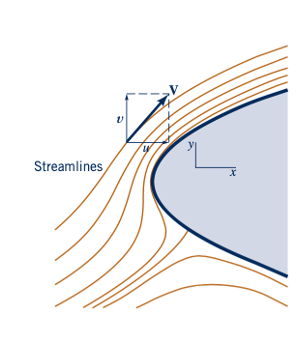
Perubahan nilai 𝜓 saat kita berpindah dari satu titik (x, y) ke titik terdekat (x + dx, y + dy) diberikan oleh hubungan:

Seiring dengan garis konstan 𝜓 kita memiliki d𝜓 ≈ 0 sehingga

dan, oleh karena itu, sepanjang garis konstan 𝜓

yang merupakan persamaan definisi untuk sebuah garis aliran. Jadi, jika kita mengetahui fungsi 𝜓(x, y), kita dapat menggambar garis-garis konstan 𝜓 untuk memberikan keluarga garis aliran yang membantu dalam memvisualisasikan pola aliran.


Sejumlah tak terbatas garis aliran membentuk medan aliran tertentu, karena untuk setiap nilai konstan yang diberikan kepada 𝜓, sebuah garis aliran dapat digambar.
Nilai numerik sebenarnya yang terkait dengan garis aliran tertentu tidaklah terlalu penting, tetapi perubahan nilai 𝜓 terkait dengan laju aliran volumetrik. Pertimbangkan dua garis aliran yang berdekatan, seperti yang ditunjukkan dalam Gambar 6.8a. Garis aliran bawah ditunjuk sebagai 𝜓 dan yang atas sebagai 𝜓 + d𝜓. Biarkan dq mewakili laju aliran volume (per satuan lebar tegak lurus terhadap bidang x–y) yang melewati di antara dua garis aliran tersebut. Perhatikan bahwa aliran tidak pernah melintasi garis aliran, karena menurut definisi, kecepatan tegak lurus terhadap garis aliran. Dari prinsip konservasi massa, kita tahu bahwa aliran masuk, dq, yang melintasi permukaan AC dalam Gambar 6.8a harus sama dengan aliran keluar bersih melalui permukaan AB dan BC. Dengan demikian,
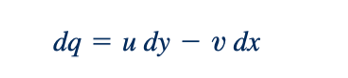
atau dalam hal fungsi aliran
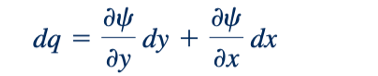
Sisi kanan dari Persamaan 6.38 sama dengan d𝜓 sehingga

Dengan demikian, laju aliran volume, q, antara dua garis aliran seperti 𝜓₁ dan 𝜓₂ pada Gambar 6.8b dapat ditentukan dengan mengintegrasikan Persamaan 6.39 untuk menghasilkan
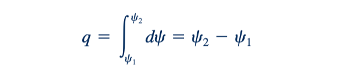

Nilai relatif 𝜓2 terhadap 𝜓1 menentukan arah aliran, seperti yang ditunjukkan oleh gambar di pinggir.
Dalam koordinat silinder, persamaan kontinuitas (Persamaan 6.35) untuk aliran dua dimensi, tidak dapat dimampatkan, menurun menjadi
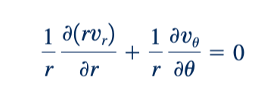
dan komponen kecepatan, vr dan vθ, dapat dihubungkan dengan fungsi aliran, 𝜓(r, θ), melalui persamaan


seperti yang ditunjukkan oleh gambar di pinggir.
Penggantian ekspresi ini untuk komponen kecepatan ke dalam Persamaan 6.41 menunjukkan bahwa persamaan kontinuitas terpenuhi secara identik. Konsep fungsi aliran dapat diperluas ke aliran simetris terhadap sumbu, seperti aliran dalam pipa atau aliran di sekitar benda putar, dan ke aliran dua dimensi yang dapat dimampatkan. Namun, konsep ini tidak berlaku untuk aliran tiga dimensi umum menggunakan satu fungsi aliran saja.

