Gaya Hidrostatik pada Permukaan Melengkung
Gaya Hidrostatik pada Permukaan Melengkung. Persamaan yang dikembangkan di Bagian 2.8 untuk magnitudo dan lokasi gaya resultant yang bertindak pada suatu permukaan tenggelam hanya berlaku untuk permukaan datar. Namun, banyak permukaan yang menarik perhatian (seperti yang terkait dengan bendungan, pipa, dan tangki) adalah non-planar. Bagian bawah berbentuk kubah dari botol minuman yang ditunjukkan dalam gambar di samping menunjukkan contoh permukaan lengkung yang khas. Meskipun gaya fluida resultant dapat ditentukan dengan integrasi, seperti yang dilakukan untuk permukaan datar, ini umumnya merupakan proses yang agak melelahkan dan tidak ada rumus sederhana dan umum yang dapat dikembangkan. Sebagai pendekatan alternatif, kita akan mempertimbangkan keseimbangan volume fluida yang dikelilingi oleh permukaan lengkung yang menarik dan proyeksi horizontal dan vertikal dari permukaan ini.
Sebagai contoh, pertimbangkan bagian lengkung dari kolam renang yang ditunjukkan dalam Gambar 2.23a. Kita ingin menemukan gaya fluida resultant yang bertindak pada bagian BC (yang memiliki panjang satuan tegak lurus terhadap bidang kertas) yang ditunjukkan dalam Gambar 2.23b. Pertama, kita isolasi sebuah volume fluida yang dibatasi oleh permukaan yang menarik perhatian, dalam kasus ini bagian BC, permukaan datar horizontal AB, dan permukaan datar vertikal AC. Diagram gaya bebas untuk volume ini ditunjukkan dalam Gambar 2.23c. Magnitudo dan lokasi gaya F1 dan F2 dapat ditentukan dari hubungan untuk permukaan datar. Berat, w, hanya berat jenis cairan dikalikan dengan volume yang terkurung dan bekerja melalui pusat gravitasi (CG) dari massa cairan yang terkandung dalam volume tersebut. Gaya FH dan FV mewakili komponen gaya yang ditanggung tangki pada cairan.
Untuk sistem gaya ini berada dalam keseimbangan, komponen horizontal FH harus memiliki magnitudo yang sama dan sejajar dengan F2, dan komponen vertikal FV harus memiliki magnitudo yang sama dengan V2.6 Botol Pop dan sejajar dengan resultant dari gaya-gaya vertikal F2 dan w. Ini mengikuti karena tiga gaya yang bertindak pada massa fluida (F2, resultant dari F1 dan w, dan gaya resultant yang ditanggung tangki pada massa) harus membentuk sistem gaya bersamaan. Artinya, dari prinsip-statika, diketahui bahwa ketika sebuah benda berada dalam keseimbangan oleh tiga gaya non-paralel, mereka harus bersamaan (garis-garis aksinya berpotongan pada satu titik yang sama) dan coplanar. Dengan demikian,
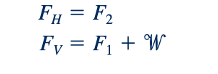
dan magnitudo resultant diperoleh dari persamaan

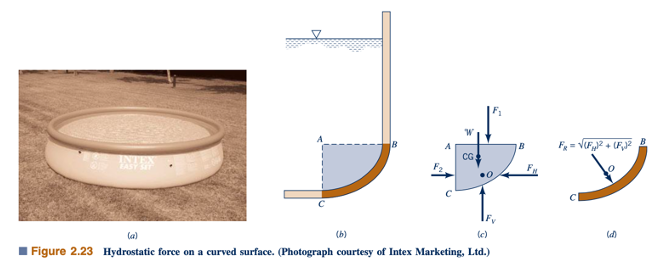
Gaya resultant FR melewati titik O, yang dapat ditemukan dengan menjumlahkan momen-momen sekitar sumbu yang sesuai. Gaya resultant dari fluida yang bertindak pada permukaan lengkung BC memiliki magnitudo yang sama dan arah yang berlawanan dengan yang diperoleh dari diagram gaya bebas pada Gambar 2.23c. Gaya fluida yang diinginkan ditunjukkan pada Gambar 2.23d.


