Gelombang Kejut Normal
Gelombang Kejut Normal. Seperti yang disebutkan sebelumnya, gelombang kejut normal dapat terjadi dalam aliran supersonik melalui saluran konvergen-divergen dan area konstan. Pengalaman masa lalu menunjukkan bahwa gelombang kejut normal melibatkan perlambatan dari aliran supersonik menjadi aliran subsonik, peningkatan tekanan, dan peningkatan entropi. Untuk mengembangkan persamaan yang memverifikasi perilaku teramati dari aliran melintasi gelombang kejut normal, kami menerapkan prinsip-prinsip dasar pada aliran melalui volume kontrol yang sepenuhnya mengelilingi gelombang kejut normal. Kami anggap gelombang kejut normal dan dengan demikian volume kontrolnya sangat tipis dan diam.
Untuk aliran stabil melalui volume kontrol Fig. 11.24, prinsip pelestarian massa menghasilkan

karena luas penampang aliran tetap secara esensial konstan dalam ketebalan infinitesimal dari gelombang kejut normal. Perhatikan bahwa Persamaan 11.134 identik dengan persamaan kontinuitas yang digunakan untuk aliran Fanno dan Rayleigh yang telah dipertimbangkan sebelumnya.
Gaya gesek yang bekerja pada isi volume kontrol yang sangat tipis yang mengelilingi gelombang kejut normal dianggap sangat kecil. Juga untuk aliran gas ideal, efek gravitasi diabaikan. Oleh karena itu, persamaan momentum linear (Eq. 5.22) yang menggambarkan aliran gas stabil melalui volume kontrol Fig. 11.24 adalah

atau untuk gas ideal di mana p=ρRT,

Persamaan 11.135 sama dengan persamaan momentum linier untuk aliran Rayleigh, yang telah diperoleh sebelumnya (Persamaan 11.111).

Untuk volume kontrol yang mengandung kejut normal, tidak ada kerja poros yang terlibat dan perpindahan panas diasumsikan tidak signifikan. Oleh karena itu, persamaan energi (Persamaan 5.692) dapat diterapkan pada aliran gas mantap melalui volume kontrol pada Gambar 11.24 untuk mendapatkan:

atau, untuk gas ideal, karena h^ − h^0 =cp (T−T0) dan p=ρRT

Persamaan 11.136 identik dengan persamaan energi untuk aliran Fanno yang dianalisis sebelumnya (Persamaan 11.75).
Hubungan Tds yang sebelumnya digunakan untuk aliran gas ideal berlaku untuk aliran melalui kejut normal (Gambar 11.24) karena itu (Persamaan 11.222) merupakan hubungan properti gas ideal.
Dari analisis pada paragraf sebelumnya, jelas bahwa aliran stabil gas ideal melintasi kejut normal diperintah oleh beberapa persamaan yang sama yang digunakan untuk menggambarkan aliran Fanno dan Rayleigh (persamaan energi untuk aliran Fanno dan persamaan momentum untuk aliran Rayleigh). Oleh karena itu, untuk suatu produk kepadatan–kecepatan tertentu (pV), gas (R, k), dan kondisi di inlet kejut normal (T, p, dan s), kondisi di hulu kejut downstream dari kejut (keadaan y) akan berada pada garis Fanno dan Rayleigh yang melalui keadaan inlet (keadaan x), seperti yang diilustrasikan di Gambar 11.25. Untuk sesuai dengan praktik umum, kita menunjukkan keadaan di hulu dan di hilir dari kejut normal dengan x dan y alih-alih angka (1 dan 2). Garis Fanno dan Rayleigh menggambarkan lebih banyak medan aliran daripada hanya di sekitar kejut normal ketika aliran Fanno dan Rayleigh benar-benar terlibat (garis solid di Gambar 11.26a dan 11.26b). Selain itu, garis-garis ini (garis putus di Gambar 11.26a, 11.26b, dan 11.26c) berguna terutama sebagai cara untuk memvisualisasikan bagaimana persamaan-persamaan pemerintah menggabungkan untuk menghasilkan solusi untuk masalah aliran kejut normal.
Hukum kedua termodinamika mensyaratkan bahwa entropi harus meningkat melintasi gelombang kejut normal. Hukum ini dan sketsa-sket Fanno line dan Rayleigh line yang bersilangan, seperti pada Gambar 11.25 dan 11.26, meyakinkan kita untuk menyimpulkan bahwa aliran melintasi kejut normal hanya dapat berlangsung dari aliran supersonik menjadi aliran subsonik. Demikian pula, dalam aliran saluran terbuka (lihat Bab 10), aliran melintasi hydraulic jump berlangsung dari kondisi superkritik menjadi subkritik.
Karena keadaan di hulu dan di hilir gelombang kejut normal diwakili oleh persimpangan supersonik dan subsonik dari Fanno line dan Rayleigh line yang nyata dan/atau dibayangkan, kita seharusnya dapat menggunakan persamaan yang dikembangkan sebelumnya untuk aliran Fanno dan Rayleigh untuk mengkuantifikasi aliran kejut normal. Sebagai contoh, untuk Rayleigh line pada Gambar 11.26b.


Tetapi dari Persamaan 11.123 untuk aliran Rayleigh, kita mendapatkan

Dan

Maka, dengan menggabungkan Persamaan 11.137, 11.138, dan 11.139 kita mendapatkan
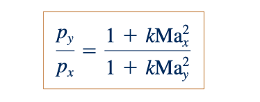
Persamaan 11.140 juga dapat diperoleh dengan memulai dari persamaan

dan menggunakan persamaan aliran Fanno (Persamaan 11.107) dalam bahasa Indonesia.

Persamaan 11.140 sebenarnya bisa diperoleh secara langsung dari persamaan momentum linier.

karena ρV2/p = V2/RT =kV2 /RTk =k Ma2.
Untuk aliran Fanno pada Gambar 11.26a,

Dari Persamaan 11.101 untuk aliran Fanno, kita mendapatkan

Dan

Sebuah konsolidasi dari Persamaan 11.141, 11.142, dan 11.143 memberikan

Kita berusaha untuk mengembangkan persamaan yang akan memungkinkan kita menentukan nomor Mach di hilir dari kejut normal, Ma 2 , ketika nomor Mach di hulu dari kejut normal, Ma 1 , diketahui. Dari persamaan keadaan gas ideal (Persamaan 11.12), kita dapat membentuk:

Dengan menggunakan persamaan kekontinuan:

dengan Persamaan 11.145, kita dapatkan:

saat digabungkan dengan definisi Mach number (Persamaan 11.462) dan persamaan kecepatan bunyi gas ideal (Persamaan 11.362), Persamaan 11.146 menjadi:

Jadi, Persamaan 11.147 dan 11.144 menghasilkan:

yang dapat digabungkan dengan Persamaan 11.140 untuk menghasilkan:
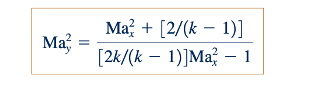

Hubungan ini digambarkan di margin untuk udara.
Dengan demikian, kita bisa menggunakan Persamaan 11.149 untuk menghitung nilai dari jumlah Mach di hulu dari sebuah kejutan normal dari jumlah Mach yang diketahui di hulu dari kejutan. Seperti yang disarankan oleh Gambar 11.26, untuk memiliki sebuah kejutan normal kita harus memiliki Max > 1. Dari Persamaan 11.149 kita temukan bahwa May < 1.
Jika kita menggabungkan Persamaan 11.149 dan 11.140, kita dapatkan:


Hubungan ini digambarkan di margin untuk udara.
Persamaan ini memungkinkan kita untuk menghitung rasio tekanan melintasi sebuah kejut normal dari sebuah Mach number aliran bagian hulu yang diketahui. Demikian juga, dengan menggabungkan Persamaan 11.149 dan 11.144 bersama-sama, kita mendapatkan


Hubungan ini digambarkan di margin untuk udara.
Dari persamaan kontinuitas (Persamaan 11.402), kita memiliki untuk aliran melintasi kejut normal

dan dari persamaan keadaan gas ideal (Persamaan 11.12)

Demikian, dengan menggabungkan Persamaan 11.152, 11.153, 11.150, dan 11.151, kita mendapatkan


Hubungan ini digambarkan di margin untuk udara.
Tekanan stagnasi yang melintasi syok dapat ditentukan dengan menggabungkan

dengan Persamaan. 11.59, 11.149, dan 11.150 untuk mendapatkan


Gambar D.4 di Lampiran D memetakan nilai-nilai downstream dari Mach numbers, May, rasio tekanan, py/px, rasio temperatur, Ty/Tx, rasio densitas, py/px, atau rasio kecepatan, Vx/Vy, dan rasio tekanan stagnasi, p0,y/p0,x, sebagai fungsi dari upstream Mach number, Max, untuk aliran steady melintasi gelombang kejut normal dari gas ideal dengan rasio panas k = 1.4. Nilai-nilai ini dihitung dari Eqs. 11.149, 11.150, 11.151, 11.154, dan 11.156.
Trend-trend penting yang terkait dengan aliran steady gas ideal melintasi gelombang kejut normal dapat ditentukan dengan mempelajari Gambar D.4. Trend-trend ini dirangkum dalam Tabel 11.3.
Contoh-contoh 11.17 dan 11.18 mengilustrasikan bagaimana Gambar D.4 dapat digunakan untuk memecahkan masalah aliran fluida yang melibatkan gelombang kejut normal.




