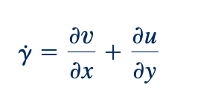Gerak Sudut dan Deformasi
Gerak Sudut dan Deformasi. Untuk kesederhanaan, kita akan mempertimbangkan gerakan dalam bidang x–y, tetapi hasilnya dapat dengan mudah diperluas ke kasus tiga dimensi yang lebih umum. Variasi kecepatan yang menyebabkan rotasi dan deformasi sudut diilustrasikan dalam Gambar 6.4a. Dalam interval waktu pendek dt, segmen garis OA dan OB akan.
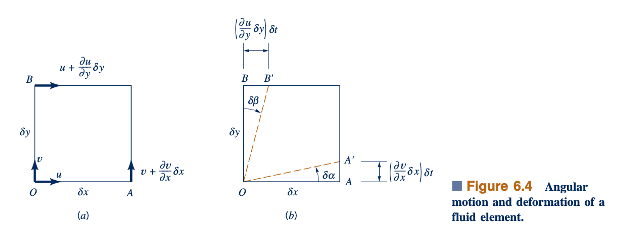
berputar melalui sudut da dan db ke posisi baru OA' dan OB', seperti yang ditunjukkan dalam Gambar 6.4b. Kecepatan sudut dari garis OA, vOA, adalah
Untuk sudut kecil
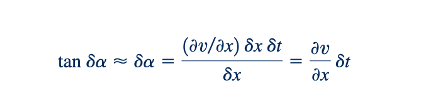
Sehingga
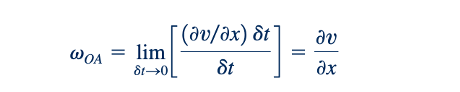
Perhatikan bahwa jika ∂v/∂x positif, vOA akan berlawanan arah jarum jam. Demikian pula, kecepatan sudut dari garis OB adalah
Dan
Sehingga
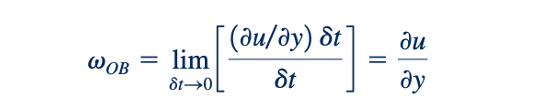
Dalam kasus ini, jika ∂u/∂y positif, vOB akan searah jarum jam. Rotasi, vz, dari elemen sekitar sumbu z didefinisikan sebagai rata-rata dari kecepatan sudut vOA dan vOB dari dua garis saling tegak lurus OA dan OB. Jadi, jika rotasi searah jarum jam dianggap positif, maka ini mengikuti bahwa
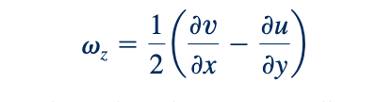
Rotasi elemen lapangan tentang dua sumbu koordinat lainnya dapat diperoleh dengan cara yang serupa dengan hasil bahwa untuk rotasi sekitar sumbu x
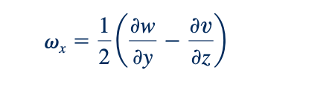
dan untuk rotasi sekitar sumbu y,
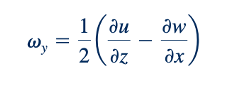
Ketiga komponen, vx, vy, dan vz dapat digabungkan untuk memberikan vektor rotasi, ω, dalam bentuk
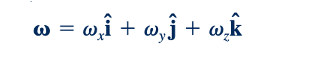
Pemeriksaan terhadap hasil ini mengungkap bahwa ω sama dengan separuh curl dari vektor kecepatan. Artinya,
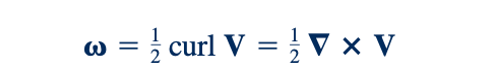
karena menurut definisi operator vektor ∇ X V,
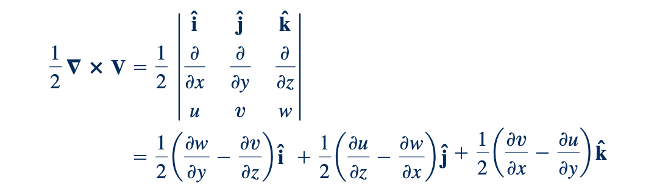
Vortisitas, Ω, didefinisikan sebagai vektor yang dua kali lipat dari vektor rotasi; dengan kata lain,
Penggunaan vortisitas untuk menjelaskan karakteristik rotasional dari fluida hanya menghilangkan faktor 1/2 yang terkait dengan vektor rotasi. Gambar di pinggiran menunjukkan kontur vortisitas dari aliran pusaran ujung sayap sesaat setelah pesawat telah lewat. Warna yang lebih terang menunjukkan vortisitas yang lebih kuat. (Lihat juga Gambar 4.3.)
Dari Persamaan 6.12, kita amati bahwa elemen fluida akan berputar sekitar sumbu z sebagai blok yang tidak terdeformasi (yaitu, vOA = ½ω vOB) hanya ketika ∂u/∂y = ½∂v/∂x. Jika tidak, rotasi akan terkait dengan deformasi sudut. Kami juga perhatikan dari Persamaan 6.12 bahwa ketika ∂u/∂y = ∂v/∂x, rotasi sekitar sumbu z adalah nol. Secara lebih umum, jika ∇ × V = 0, maka rotasi (dan vortisitas) adalah nol, dan medan aliran untuk kondisi ini disebut irrotasional. Kita akan temukan di Bagian 6.4 bahwa kondisi irrotasionalitas sering sangat menyederhanakan analisis medan aliran yang kompleks. Namun, mungkin tidak langsung jelas mengapa beberapa medan aliran akan irrotasional, dan kita perlu memeriksa konsep ini lebih lanjut di Bagian 6.4.
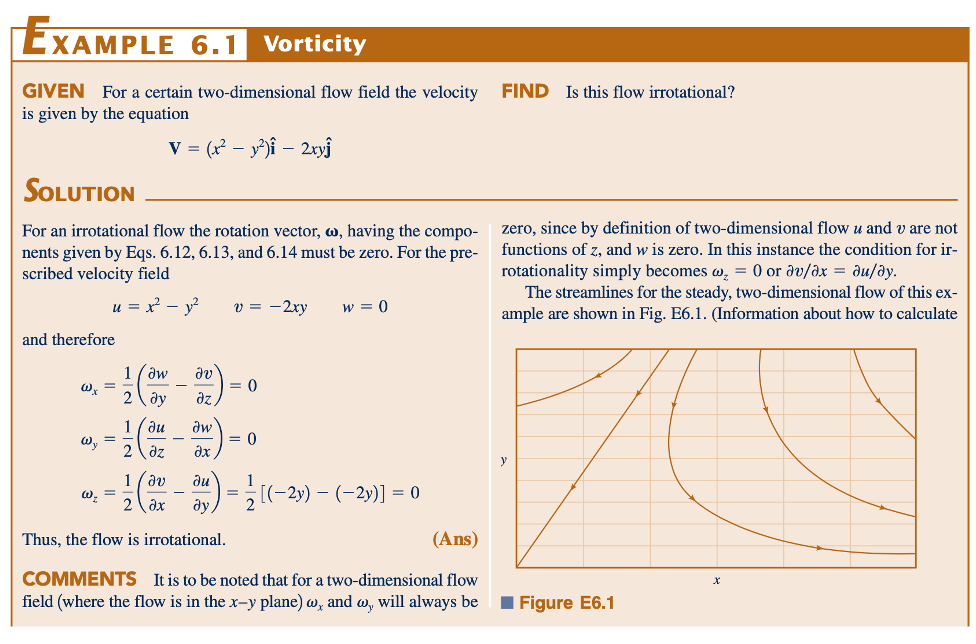
Selain rotasi yang terkait dengan turunan ∂u/∂y dan ∂v/∂x, diamati dari Gambar 6.4b bahwa turunan-turunan ini dapat menyebabkan elemen fluida mengalami deformasi sudut, yang mengakibatkan perubahan bentuk elemen. Perubahan sudut siku-siku awal yang terbentuk oleh garis-garis OA dan OB disebut regangan geser, γ, dan dari Gambar 6.4b
dianggap positif jika sudut siku-siku awal berkurang. Laju perubahan dg disebut laju regangan geser atau laju deformasi sudut dan umumnya dilambangkan dengan simbol γ-dot. Sudut-sudut da dan db terkait dengan gradien kecepatan melalui Persamaan 6.10 dan 6.11 sehingga
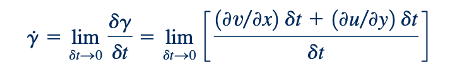
dan, oleh karena itu,
