12.5 Hubungan NVF-TVD
Hubungan NVF-TFD. Kedua formulasi NVF dan TVD menerapkan Keterbatasan dengan pendekatan yang berbeda, yang dapat ditunjukkan memiliki hubungan yang agak terkait. Ini dilakukan dengan pertama-tama mendapatkan hubungan antaradan
kemudian membandingkan NVF-CBC (Persamaan 12.13) dengan TVD-CBC (Persamaan 12.40), dan akhirnya menyajikan transformasi umum yang memungkinkan hubungan fungsional dari skema TVD apa pun ditulis dalam kerangka kerja NVF dan sebaliknya.
Hubungan antara dan
dapat dengan mudah diperoleh dengan memulai dari definisi
dan diperoleh sebagai:
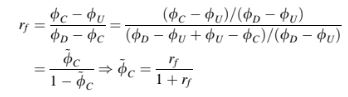
Dengan menggunakan Persamaan (12.45), sejumlah skema linear dapat dibandingkan dalam dua kerangka kerja tersebut. Pembatas yang mewakili skema Upwind dalam formulasi TVD juga setara dengan skema upwind dalam formulasi NVF (yaitu,
). Ini mengikuti dari fakta bahwa
Skema upwind diberlakukan sebagai batas untuk TVD-CBC ketika
kondisi yang setara dalam NVF-CBC diperoleh sebagai:
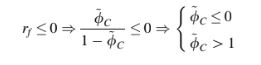
Ini juga mewakili kondisi untuk menerapkan skema Upwind dalam NVF-CBC. Selain itu, pada NVF-CBC, hubungan fungsional harus meningkat monoton di wilayah Pada diagram Sweby, wilayah tersebut meluas di selang
Kedua wilayah tersebut mewakili interval yang sama seperti yang ditunjukkan oleh hubungan berikut:
Selanjutnya, untuk kondisi TVD-CBC
Kondisi yang setara dalam NVF-CBC dapat diperoleh sebagai berikut:
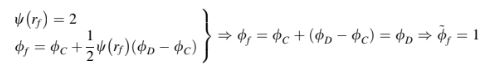
Oleh karena itu,
Kondisi terakhir yang diberlakukan oleh TVD-CBC pada diberikan oleh
Kondisi setara menggunakan NVF-CBC diperoleh sebagai
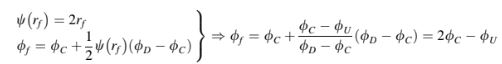
yang dapat dinormalisasi untuk menghasilkan
Ini lebih membatasi daripada NVF-CBC dan merupakan satu-satunya perbedaan antara kedua formulasi tersebut. Berdasarkan kondisi ini, TVD-CBC dan NVF-CBC yang dimodifikasi akan terlihat seperti yang ditunjukkan dalam Gambar 12.14a dengan wilayah monoton yang berkurang menjadi garis upwind dan area biru. Sementara TVD-CBC yang dimodifikasi dan NVF-CBC (yaitu, kondisi pada NVF-CBC bersesuaian dengan
pada TVD-CBC) akan terlihat seperti yang ditunjukkan dalam Gambar 12.14b. Mengenai akurasi orde kedua, dikatakan bahwa untuk skema TVD agar akurat orde kedua, harus melewati titik (1, 1), yaitu
Nilai-nilai setara menggunakan NVF ditemukan sebagai,
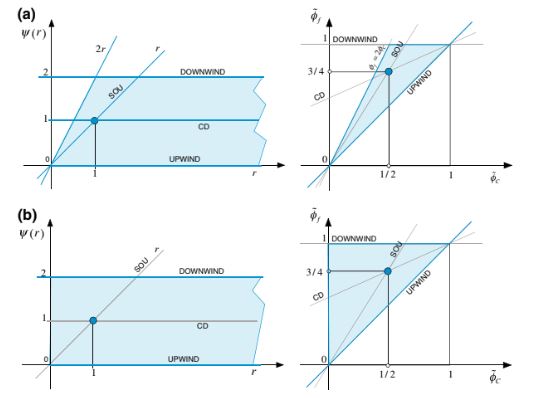
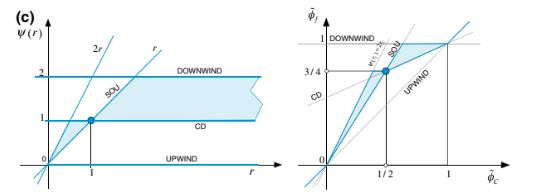
Gambar 12.14 a TVD-CBC pada Diagram Sweby dan Variabel Dinormalisasi. b NVF-CBC pada Diagram Sweby dan Variabel Dinormalisasi. c TVD-CBC pada Diagram Sweby dan Variabel Dinormalisasi untuk skema orde kedua.
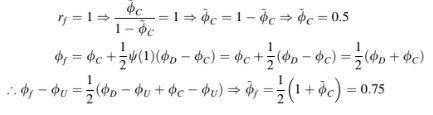
Seperti yang disebutkan sebelumnya, Van Leer mendemonstrasikan bahwa setiap skema orde kedua dapat ditulis sebagai rata-rata tertimbang dari skema CD dan SOU. Oleh karena itu, hubungan fungsionalnya harus berada di antara hubungan fungsional dari skema CD dan SOU dengan wilayah monotonik TVD-CBC mereka dikurangi menjadi garis upwind dan area biru yang ditunjukkan pada diagram Sweby dan NVD dalam Gambar 12.14c.
Prosedur di atas dapat digeneralisasi untuk mentransformasikan setiap skema TVD menjadi skema NVF yang setara dan sebaliknya. Mulai dengan skema dalam kerangka kerja NVF, nilai di wajahdiungkapkan sebagai,
sedangkan untuk skema TVD diberikan oleh
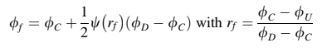
Menyeimbangkan kedua persamaandi atas, menghasilkan
oleh karena itu
Suku di sisi kiri persamaan di atas dapat dimodifikasi menjadi
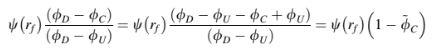
mengarah ke
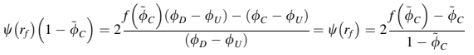
Persamaan (12.60) juga dapat ditulis sebagai
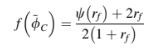
Sebagai contoh, hubungan fungsional skema UPWIND dalam kerangka kerja NVF adalah pembatas TVD-nya ditemukan sebagai
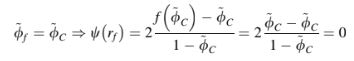
Pembatas TVD untuk skema DOWNWIND adalah hubungan fungsional NVF-nya dapat diperoleh sebagai,
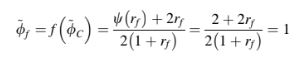
Mengetahui bentuk NVF dari skema SOU, pembatas TVD-nya dihitung sebagai
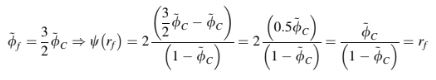
Hal yang sama berlaku untuk skema lainnya.
