Interpolasi Rhie-Chow
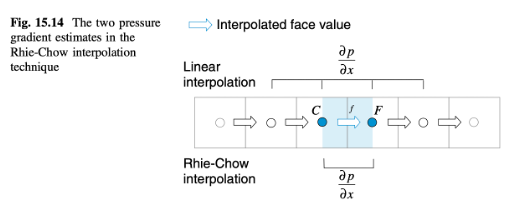
Interpolasi Rhie-Chow. Kelemahan dalam formulasi kolokasi asli yang disajikan sebelumnya terletak pada interpolasi linear yang digunakan untuk menghitung kecepatan di wajah elemen. Interpolasi ini mengakibatkan dekopling nilai tekanan dan kecepatan pada tingkat sel yang menghasilkan masalah papan catur. Pada tahun 1983, Rhie dan Chow melaporkan tentang prosedur interpolasi yang memungkinkan formulasi algoritma SIMPLE pada kisi kolokasi. Dalam metode mereka, sebuah istilah disipasi, yang mewakili perbedaan antara dua estimasi gradien tekanan wajah sel, ditambahkan ke kecepatan sel wajah yang diinterpolasi secara linier. Seperti yang ditunjukkan dalam Gambar 15.14, dua estimasi gradien tekanan didasarkan pada stensil grid yang berbeda.
Prosedur ini akan terbukti setara dengan membangun persamaan pseudo-momentum di wajah elemen dengan koefisiennya diinterpolasi secara linear dari koefisien persamaan momentum di pusat elemen yang menjulur di wajah dan gradien tekanan dihitung menggunakan stensil grid kecil. Dalam hal itu, interpolasi Rhie-Chow hanya meniru koneksi tekanan-kecepatan stensil kecil dari susunan kisi terhampar.
Dimulai dengan persamaan momentum x yang terdiskritisasi untuk sel C dan F, yang dipresentasikan sebelumnya sebagai:

Sebuah persamaan kecepatan u-f yang mirip dengan persamaan (15.50), dengan gradien tekanan yang terhubung ke nilai tekanan tetangga lokal, seperti yang diilustrasikan dalam Gambar 15.14, akan memiliki bentuk berikut:

Karena dalam kisi kolokasi, koefisien persamaan ini tidak dapat dihitung secara langsung, mereka diaproksimasi dengan interpolasi dari koefisien simpul tetangga. Dengan menggunakan profil interpolasi linier, koefisien ini dihitung sebagai:

Dengan menggunakan nilai yang diberikan dalam Persamaan (15.52), persamaan pseudo-momentum di wajah elemen menjadi:

Ini adalah dalam segala hal persamaan momentum pada kisi "terhampar", yang direkonstruksi menggunakan koefisien momentum kisi yang terletak.
Dalam semua persamaan di atas dan untuk penggunaan selanjutnya, nilai dengan garis atas diperoleh dengan interpolasi linear antara nilai pada titik C dan F sesuai dengan

di mana gC dan gF adalah faktor interpolasi geometris yang terkait dengan posisi wajah elemen f terhadap simpul C dan F, seperti yang dijelaskan dalam bab-bab sebelumnya.
Menggunakan Persamaan (15.50), Hf dapat ditulis ulang sebagai
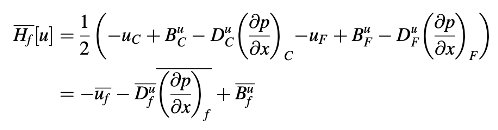
di mana estimasi koefisien dapat ditunjukkan sebagai akurat orde kedua, yaitu:

Dengan mengganti Persamaan (15.55) ke dalam Persamaan (15.53), kecepatan di wajah elemen menggunakan metode interpolasi Rhie-Chow diperoleh sebagai:

Untuk situasi multidimensional, rumus interpolasi serupa dapat diturunkan untuk komponen kecepatan y dan z dan diberikan oleh

Persamaan (15.57) - (15.59) dapat dituliskan dalam bentuk vektor, yang lebih sesuai untuk menurunkan persamaan koreksi tekanan multidimensi, sebagai:

Dimana

dan di mana ∇pf dihitung seperti yang dijelaskan di Bagian 9.4 menggunakan

dan menghasilkan stensil dalam arah CF yang terbentuk hanya dari nilai sel tetangga pF dan pC sebagai

