Kecepatan Gelombang
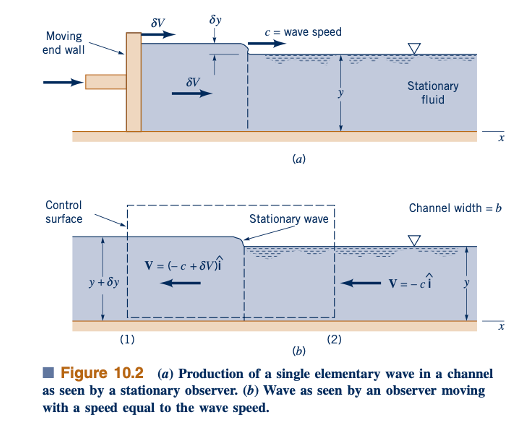
Kecepatan Gelombang. Pertimbangkan situasi yang diilustrasikan dalam Gambar 10.2a di mana gelombang elementer tunggal dengan ketinggian kecil, 𝛿y, dihasilkan di permukaan saluran oleh pergerakan mendadak dinding akhir yang awalnya diam dengan kecepatan 𝛿V. Air di dalam saluran diam pada waktu awal, t = 0. Seorang pengamat diam akan melihat satu gelombang bergerak turun saluran dengan kecepatan gelombang c, tanpa gerakan fluida di depan gelombang dan kecepatan fluida 𝛿V di belakang gelombang. Gerakan ini bersifat tidak tetap bagi pengamat seperti itu. Bagi seorang pengamat yang bergerak sepanjang saluran dengan kecepatan c, aliran akan terlihat tetap seperti yang ditunjukkan dalam Gambar 10.2b. Bagi pengamat tersebut, kecepatan fluida akan menjadi V = c^i di sebelah kanan pengamat dan V = (1+c - 𝛿V)^i di sebelah kiri pengamat.
Hubungan antara berbagai parameter yang terlibat dalam aliran ini dapat diperoleh dengan menerapkan persamaan kontinuitas dan momentum pada volume kontrol yang ditunjukkan dalam Gambar 10.2b sebagai berikut. Dengan asumsi aliran satu dimensi yang seragam, persamaan kontinuitas menjadi:

di mana b adalah lebar saluran. Ini disederhanakan menjadi:
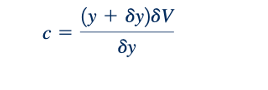
atau dalam batas gelombang amplitudo kecil dengan 𝛿𝑦 ≪ 𝑦

Demikian pula, persamaan momentum (Pers. 5.22) adalah:
dengan asumsi bahwa laju aliran massa ditulis sebagai m=ρbcy dan telah diasumsikan bahwa variasi tekanan bersifat hidrostatik dalam fluida. Artinya, gaya tekanan pada penampang lintang saluran 1 dan 2 adalah F=ρgyA−ρg(y+dy)A=ρgA(dy) dan F=ρgyA−ρgyA=0, secara berurutan. Jika kita lagi mengasumsikan gelombang amplitudo kecil [yaitu (𝛿𝑦)2 ≪ 𝑦 𝛿y], maka persamaan momentum menyederhanakan menjadi

Kombinasi Persamaan 10.1 dan 10.2 memberikan kecepatan gelombang

Kecepatan gelombang dalam amplitudo kecil seperti yang ditunjukkan dalam Gambar 10.2 proposional dengan akar kuadrat kedalaman fluida, y, dan tidak tergantung pada amplitudo gelombang, 𝛿𝑦. Kepadatan fluida bukan parameter penting, meskipun percepatan gravitasi adalah. Hal ini disebabkan oleh fakta bahwa gerakan gelombang merupakan keseimbangan antara efek inersial (yang proposional dengan p) dan efek berat atau tekanan hidrostatik (yang proposional dengan y = pg). Rasio dari gaya-gaya ini menghilangkan faktor umum ρ tetapi tetap mempertahankan g. Untuk gelombang yang sangat kecil (seperti yang dihasilkan oleh serangga di atas air seperti yang ditunjukkan dalam Video V10.3), Persamaan 10.3 tidak berlaku karena efek tegangan permukaan yang signifikan.
Kecepatan gelombang juga dapat dihitung dengan menggunakan persamaan energi dan kontinuitas daripada persamaan momentum dan kontinuitas seperti yang dilakukan di atas. Sebuah gelombang sederhana pada permukaan ditunjukkan dalam Gambar 10.3. Seperti yang terlihat oleh pengamat yang bergerak dengan kecepatan gelombang, c, aliran ini adalah steady. Karena tekanan konstan pada setiap titik pada permukaan bebas, persamaan Bernoulli untuk aliran tanpa gesekan ini adalah:

atau dengan membedakan
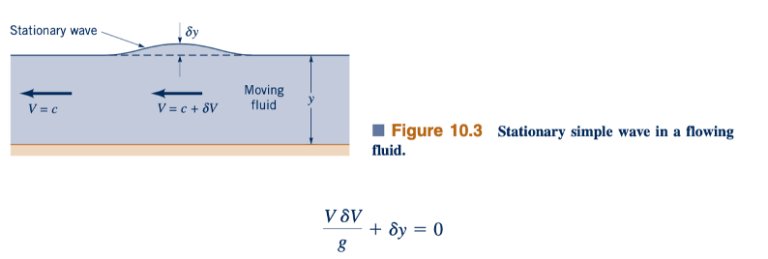
Juga, dengan mengalikan persamaan kontinuitas Vy=konstan, kita dapatkan:
Kita gabungkan kedua persamaan tersebut untuk menghilangkan 𝛿V dan 𝛿y dan gunakan fakta bahwa V=c untuk situasi ini (pengamat bergerak dengan kecepatan c) untuk mendapatkan kecepatan gelombang yang diberikan oleh Persamaan 10.3.
Hasil di atas dibatasi pada gelombang beramplitudo kecil karena kita telah mengasumsikan aliran satu dimensi. Artinya,𝛿y/y ≪ 1. Analisis dan eksperimen yang lebih lanjut menunjukkan bahwa kecepatan gelombang untuk gelombang soliter berukuran terbatas melebihi yang diberikan oleh Persamaan 10.3. Pada pendekatan pertama, seseorang memperoleh (Ref. 42)
Ini menunjukkan bahwa persamaan yang kita gunakan memiliki batasan pada gelombang dengan amplitudo yang kecil, di mana asumsi aliran satu dimensi tetap berlaku. Analisis yang lebih lanjut dan eksperimen menunjukkan bahwa untuk gelombang soliter berukuran yang lebih besar, kecepatan gelombang melebihi prediksi dari Persamaan 10.3. Secara kasar, perhitungan yang lebih canggih dapat memberikan hasil yang lebih akurat untuk gelombang-gelombang tersebut. Referensi 42 dapat memberikan informasi lebih lanjut tentang hal ini.

Seperti yang ditunjukkan oleh gambar di pinggiran, semakin besar amplitudo, semakin cepat gelombang bergerak.
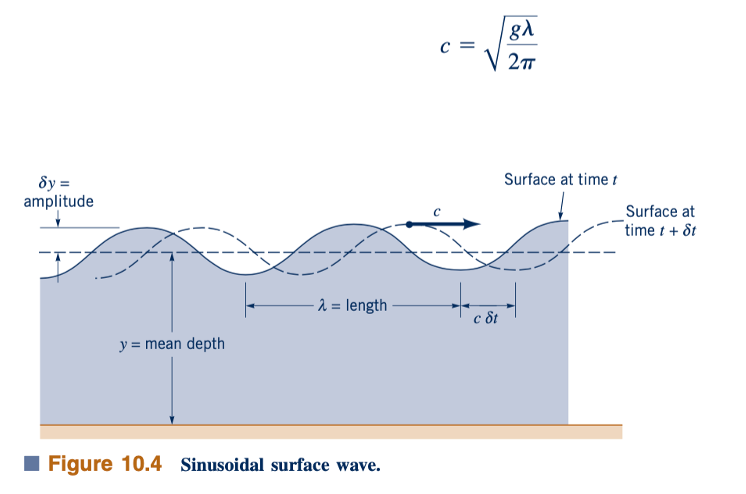
Deskripsi yang lebih umum tentang gerakan gelombang dapat diperoleh dengan mempertimbangkan gelombang kontinu (bukan soliter) berbentuk sinusoidal seperti yang ditunjukkan dalam Gambar 10.4. Dengan menggabungkan gelombang-gelombang dengan panjang gelombang, λ, dan amplitudo, 𝛿y, yang berbeda, adalah mungkin untuk menggambarkan pola permukaan yang sangat kompleks yang ditemukan di alam, seperti gelombang yang disebabkan oleh angin di atas sebuah danau. Secara matematis, proses tersebut melibatkan penggunaan deret Fourier (setiap suku dalam deret tersebut direpresentasikan oleh gelombang dengan panjang gelombang dan amplitudo yang berbeda) untuk merepresentasikan fungsi arbitrer (bentuk permukaan bebas).
Analisis yang lebih canggih dari gelombang permukaan sinusoidal dengan amplitudo kecil seperti itu menunjukkan bahwa kecepatan gelombang bervariasi dengan panjang gelombang dan kedalaman fluida, sesuai dengan (Ref. 1).
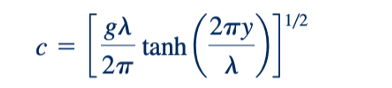
Di mana tanh (2𝜋𝑦/𝜆) adalah tangen hiperbolik dari argumen (2𝜋𝑦/𝜆). Hasilnya dipetakan dalam Gambar 10.5. Untuk kondisi di mana kedalaman air jauh lebih besar dari panjang gelombang (𝑦 ≫ 𝜆, seperti di laut), kecepatan gelombang tidak tergantung pada y dan diberikan oleh

Hasil ini, yang ditunjukkan dalam gambar di sisi, mengikuti dari Persamaan 10.4, karena tanh(2𝜋𝑦/𝜆) 𝜆→1 saat 𝑦/𝜆 ∞ mendekati 0. Perhatikan bahwa gelombang dengan panjang gelombang yang sangat panjang [misalnya, gelombang yang diciptakan oleh tsunami ("gelombang pasang") dengan panjang gelombang sekitar beberapa kilometer] bergerak sangat cepat. Di sisi lain, jika lapisan fluida dangkal (𝑦 ≫ 𝜆, seperti yang sering terjadi di saluran terbuka), kecepatan gelombang diberikan oleh c =(gy)1/2), seperti yang dihasilkan untuk gelombang soliter di Gambar 10.2. Hasil ini juga mengikuti dari Persamaan 10.4, karena tanh (2𝜋𝑦/𝜆) → 2𝜋𝑦/𝜆 saat 𝑦/𝜆 → 0. Dua kasus terbatas ini ditunjukkan dalam Gambar 10.5. Untuk lapisan kedalaman moderat (𝑦~𝜆) , hasilnya diberikan oleh Persamaan lengkap 10.4. Perhatikan bahwa untuk kedalaman fluida tertentu, gelombang panjang bergerak paling cepat. Oleh karena itu, untuk tujuan kami, kita akan mempertimbangkan kecepatan gelombang adalah situasi batas ini, c = (gy)1/2).

