Kerugian Besar
Pendekatan analisis dimensional dari aliran pipa memberikan dasar yang paling nyaman untuk mempertimbangkan aliran pipa yang turbulen dan sepenuhnya berkembang. Pengantar untuk topik ini telah diberikan dalam Bagian 8.3. Seperti yang dibahas dalam Bagian 8.2.1 dan 8.2.4, penurunan tekanan dan kehilangan head dalam pipa tergantung pada gaya geser dinding, τw , antara fluida dan permukaan pipa. Perbedaan mendasar antara aliran laminar dan turbulen adalah bahwa gaya geser untuk aliran turbulen adalah fungsi dari kerapatan fluida, ρ. Untuk aliran laminar, gaya geser tidak tergantung pada kerapatan, meninggalkan viskositas, μ, sebagai satu-satunya properti fluida yang penting.
Dengan demikian, seperti yang ditunjukkan oleh gambar di pinggir, penurunan tekanan, Δp, untuk aliran turbulen, stabil, tak dapat dikompres, dalam pipa bulat horizontal berdiameter D dapat ditulis dalam bentuk fungsional sebagai
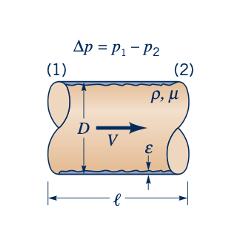
di mana V adalah kecepatan rata-rata, L adalah panjang pipa, dan e adalah ukuran kasar permukaan pipa. Jelas bahwa Δp seharusnya merupakan fungsi dari V, D, dan e. Ketergantungan Δp pada sifat-sifat fluida μ dan ρ diharapkan karena ketergantungan t pada parameter-parameter ini.
Meskipun penurunan tekanan untuk aliran pipa laminar ditemukan tidak bergantung pada kasar permukaan pipa, perlu untuk menyertakan parameter ini ketika mempertimbangkan aliran turbulen. Seperti dibahas di Bagian 8.3.3 dan diilustrasikan dalam Gambar 8.19, untuk aliran turbulen terbentuk lapisan viskos yang relatif tipis di fluida dekat dinding pipa. Dalam banyak kasus lapisan ini sangat tipis; d = D di mana d adalah ketebalan lapisan sub, dan D adalah diameter pipa. Jika suatu elemen kasar permukaan pipa biasa menonjol cukup jauh ke dalam 1atau bahkan melalui2 lapisan ini, struktur dan properti lapisan viskos (bersama dengan Δp dan τw) akan berbeda daripada jika dindingnya halus. Oleh karena itu, untuk aliran turbulen penurunan tekanan diharapkan menjadi fungsi dari kasar permukaan dinding. Untuk aliran laminar tidak ada lapisan viskos yang tipis - efek viskos penting di seluruh pipa. Dengan demikian, elemen kasar permukaan yang relatif kecil memiliki efek yang sepenuhnya tidak signifikan pada aliran pipa laminar. Tentu saja, untuk pipa dengan "kasar" dinding yang sangat besar (𝜀/D ≥ 0.12), seperti yang ada pada pipa berlapis, laju aliran mungkin menjadi fungsi dari "kasarannya". Kami hanya akan mempertimbangkan pipa konstan diameter khas dengan kasar relatif dalam kisaran 0 ≤ 𝜀/D ≤ 0.05. Analisis aliran dalam pipa berlapis tidak masuk ke dalam kategori pipa diameter konstan standar, meskipun hasil eksperimental untuk pipa-pipa tersebut tersedia.
Daftar parameter yang diberikan dalam Persamaan 8.32 nampaknya lengkap. Artinya, eksperimen telah menunjukkan bahwa parameter lain 1seperti tegangan permukaan, tekanan uap, dll.2 tidak memengaruhi penurunan tekanan untuk kondisi yang dinyatakan 1aliran mantap, inkompresibel; pipa horizontal, bulat2. Karena ada tujuh variabel (k = 7) yang dapat ditulis dalam bentuk tiga dimensi referensi MLT (r = 3), Persamaan 8.32 dapat ditulis dalam bentuk tak berdimensi dengan menggunakan k-r = 4 kelompok tak berdimensi. Seperti yang dibahas di Bagian 7.9.1, satu representasi tersebut adalah:
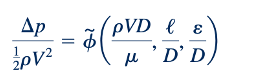
Hasil ini berbeda dari yang digunakan untuk aliran laminar 1lihat Persamaan 8.172) dalam dua hal. Pertama, kita memilih untuk membuat tekanan tak berdimensi dengan membaginya dengan tekanan dinamis, ρV2 , daripada tekanan geser viskositas karakteristik, μ DV . Konvensi ini dipilih dengan mengakui bahwa tekanan geser untuk aliran turbulen biasanya didominasi oleh τ turb , yang merupakan fungsi yang lebih kuat

Hal kedua, kami memperkenalkan dua parameter tak berdimensi tambahan, yaitu jumlah Reynolds, Re= μrVD , dan kekasaran relatif, De , yang tidak ada dalam formulasi laminar karena dua parameter r dan e tidak penting dalam aliran pipa laminar yang sudah berkembang sepenuhnya.
Seperti yang dilakukan untuk aliran laminar, representasi fungsional dapat disederhanakan dengan memberlakukan asumsi yang masuk akal bahwa penurunan tekanan harus berbanding lurus dengan panjang pipa. Langkah seperti ini tidak termasuk dalam domain analisis dimensional. Ini hanyalah asumsi logis yang didukung oleh eksperimen. Satu-satunya cara agar ini benar adalah jika ketergantungan D/L difaktorkan keluar sebagaimana
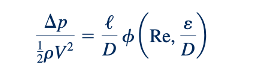
Seperti yang dibahas dalam Bagian 8.2.3, kuantitas ΔpD (ℓρV2/2) disebut faktor gesekan, f. Oleh karena itu, untuk pipa horizontal, persamaan (\ref{eq:8.33}) dapat ditulis ulang dalam bentuk f.
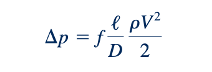
Dimana
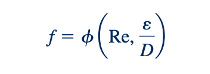
Untuk aliran laminar yang sepenuhnya berkembang, nilai f secara sederhana adalah f= 64/Re , independen dari 𝜀/D. Untuk aliran turbulen, ketergantungan fungsional faktor gesekan terhadap jumlah Reynolds dan ketebalan relatif, f=f(Re,𝜀/D), adalah kompleks dan belum dapat diperoleh dari analisis teoritis. Hasil ini diperoleh dari serangkaian eksperimen yang memadai dan biasanya disajikan dalam bentuk rumus penyesuaian kurva atau bentuk grafis yang setara.
Dari Persamaan 5.89, persamaan energi untuk aliran tak berkompressibel yang stabil adalah:
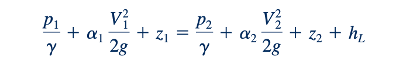
di mana h adalah kehilangan head antara bagian (1) dan (2). Dengan asumsi diameter konstan (D1=D2 sehingga V1=V2) , pipa horizontal (z1=z2) dengan aliran yang sepenuhnya (𝛼1- 𝛼2) berkembang, ini menjadi Δp=p1 −p2 =ρ𝛾hL , yang dapat digabungkan dengan Persamaan 8.33 untuk memberikan:

Persamaan 8.34, yang disebut persamaan Darcy–Weisbach, berlaku untuk aliran pipa yang sepenuhnya berkembang, stabil, dan tak berkompressibel—baik pipanya horizontal maupun di atas bukit. Di sisi lain, Persamaan 8.33 hanya berlaku untuk pipa horizontal. Secara umum, dengan V1 =V2 , persamaan energi memberikan:
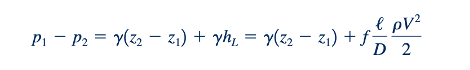
Sebagian dari perubahan tekanan disebabkan oleh perubahan elevasi dan sebagian lagi disebabkan oleh hilangnya head terkait dengan efek gesekan, yang dinyatakan dalam bentuk faktor gesekan, f.
Tidak mudah untuk menentukan ketergantungan fungsional dari faktor gesekan terhadap nomor Reynolds dan kekasaran relatif. Sebagian besar informasi ini adalah hasil dari eksperimen yang dilakukan oleh J. Nikuradse pada tahun 1933 dan diperluas oleh banyak orang lain sejak saat itu. Salah satu kesulitan terletak pada penentuan kekasaran pipa. Nikuradse menggunakan pipa yang diroughening secara artifisial dengan menempelkan butiran pasir berukuran diketahui ke dinding pipa untuk menghasilkan pipa dengan permukaan seperti kertas amplas. Penurunan tekanan yang dibutuhkan untuk menghasilkan laju aliran yang diinginkan diukur, dan data tersebut dikonversi menjadi faktor gesekan untuk nomor Reynolds dan kekasaran relatif yang sesuai. Pengujian ini diulang berkali-kali untuk rentang Re dan 𝜀/D yang luas untuk menentukan ketergantungan f pada f(Re,𝜀/D).
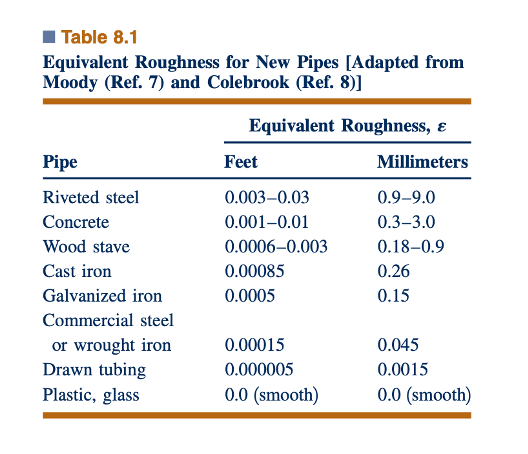
Di pipa yang tersedia secara komersial, kekasaran tidak seuniform dan sejelas pada pipa yang diroughening secara artifisial yang digunakan oleh Nikuradse. Namun, memungkinkan untuk memperoleh ukuran kekasaran relatif efektif dari pipa-pipa tipikal dan dengan demikian memperoleh faktor gesekan. Nilai-nilai kekasaran tipikal untuk berbagai permukaan pipa diberikan dalam Tabel 8.1. Gambar 8.20 menunjukkan ketergantungan fungsional dari f terhadap Re dan 𝜀/D dan disebut Moody chart untuk menghormati L. F. Moody, yang bersama dengan C. F. Colebrook, mengkorelasikan data asli Nikuradse dalam hal kekasaran relatif dari bahan pipa yang tersedia secara komersial. Harus diingat bahwa nilai-nilai 𝜀/D tidak selalu sesuai dengan nilai-nilai sebenarnya yang diperoleh dengan penentuan mikroskopis dari tinggi rata-rata kekasaran permukaan. Namun, mereka memberikan korelasi yang benar untuk f terhadap f(Re,𝜀/D).
Penting untuk diperhatikan bahwa nilai-nilai kekasaran relatif yang diberikan berkaitan dengan pipa baru dan bersih. Setelah penggunaan yang cukup lama, sebagian besar pipa (karena penumpukan korosi atau skala) mungkin memiliki kekasaran relatif yang jauh lebih besar (mungkin dengan satu orde besarnya) daripada yang diberikan. Seperti yang ditunjukkan oleh gambar di atas, pipa-pipa yang sangat tua dapat memiliki penumpukan skala yang cukup untuk tidak hanya mengubah nilai 𝜀 tetapi juga mengubah diameter efektif mereka dengan jumlah yang cukup besar.
Karakteristik berikut diamati dari data Gambar 8.20. Untuk aliran laminar, f= 64/Re, yang independen dari kekasaran relatif. Untuk aliran turbulent dengan nomor Reynolds yang sangat besar, (f= 𝜙(𝜀/D), yang, seperti yang ditunjukkan oleh gambar di atas, independen dari nomor Reynolds. Untuk aliran seperti itu, umumnya disebut sebagai aliran sepenuhnya turbulent, lapisan sub-laminar sangat tipis (ketebalannya berkurang dengan peningkatan Re) sehingga kekasaran permukaan sepenuhnya mendominasi karakter aliran di dekat dinding. Oleh karena itu, penurunan tekanan yang diperlukan merupakan sebuah
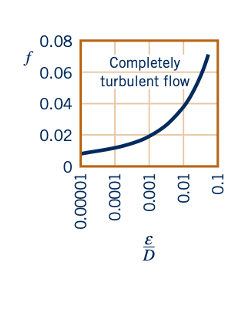

Hasil dari tekanan geser turbulent yang didominasi oleh inersia daripada tekanan geser laminar yang didominasi oleh viskositas biasanya ditemukan dalam lapisan sub-laminar. Untuk aliran dengan nilai Re moderat, faktor gesekan memang bergantung pada nomor Reynolds dan kekasaran relatif (f= f(Re,𝜀/D). Celah dalam gambar di mana tidak ada nilai f yang diberikan (rentang 2100≤Re≤4000) adalah hasil dari kenyataan bahwa aliran dalam rentang transisi ini dapat menjadi laminar atau turbulent (atau campuran tidak stabil dari keduanya) tergantung pada keadaan khusus yang terlibat.
Perhatikan bahwa bahkan untuk pipa yang halus (𝜀 = 0), faktor gesekan tidak nol. Artinya, ada kehilangan kepala di dalam pipa apa pun, tidak peduli seberapa halus permukaannya dibuat. Hal ini merupakan hasil dari kondisi batas no-slip yang mengharuskan fluida untuk melekat pada permukaan padat yang dilaluinya. Selalu ada sedikit kekasaran permukaan mikroskopis yang menghasilkan perilaku no-slip (dan dengan demikian f ≠ 0) pada tingkat molekuler, bahkan ketika kekasarannya jauh lebih kecil dari ketebalan lapisan sub-laminar. Pipa-pipa seperti ini disebut halus secara hidrolik.
Berbagai peneliti telah berusaha untuk mendapatkan ekspresi analitis untuk (f=𝜙(Re,𝜀/D). Perlu diperhatikan bahwa diagram Moody mencakup rentang yang sangat luas dalam parameter aliran. Wilayah non-laminar mencakup lebih dari empat deret Reynolds—dari Re=4×10 (3) hingga Re=10 8 . Tentu saja, untuk pipa dan fluida tertentu, nilai tipikal dari kecepatan rata-rata tidak mencakup rentang ini. Namun, karena variasi besar dalam pipa (diameter), fluida (kepadatan dan viskositas), dan kecepatan, rentang yang luas dalam Re diperlukan untuk mencakup hampir semua aplikasi aliran pipa. Dalam banyak kasus, aliran pipa yang menarik terbatas pada wilayah yang relatif kecil dari diagram Moody, dan ekspresi semi-empiris sederhana dapat dikembangkan untuk kondisi tersebut. Sebagai contoh, sebuah perusahaan yang memproduksi pipa air besi cor dengan diameter antara 2 dan 12 inci mungkin menggunakan persamaan sederhana yang hanya berlaku untuk kondisi mereka. Diagram Moody, di sisi lain, berlaku secara universal untuk semua aliran pipa yang steady, sepenuhnya berkembang, dan tak terkompressi.
Persamaan berikut dari Colebrook berlaku untuk seluruh rentang nonlaminar dari diagram Moody.

Sebenarnya, diagram Moody adalah representasi grafis dari persamaan ini, yang merupakan hasil perumusan empiris dari data tekanan drop aliran pipa. Persamaan 8.35 disebut sebagai formula Colebrook. Kendala dalam penggunaannya adalah bahwa hubungan f bersifat implisit. Artinya, untuk kondisi tertentu (Re dan 𝜀/D), tidak mungkin untuk menyelesaikan f tanpa skema iteratif tertentu. Dengan menggunakan komputer dan kalkulator modern, perhitungan semacam itu tidak sulit. Perlu diingat bahwa penggunaan diagram Moody atau formula Colebrook yang setara memerlukan kewaspadaan. Karena beberapa ketidakpastian yang melekat (ketidakpastian dalam relatif kasar, ketidakpastian dalam data eksperimental yang digunakan untuk menghasilkan diagram Moody, dll.), penggunaan beberapa tempat desimal dalam masalah aliran pipa biasanya tidak beralasan. Aturan praktisnya, akurasi sebesar 10% adalah yang terbaik yang dapat diharapkan. Memungkinkan untuk mendapatkan persamaan yang secara memadai mendekati hubungan diagram Colebrook-Moody namun tidak memerlukan skema iteratif. Sebagai contoh, persamaan Haaland (Ref. 34), yang lebih mudah digunakan, diberikan oleh
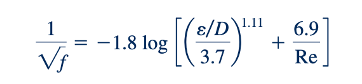
di mana seseorang dapat menyelesaikan f secara eksplisit.


