Kerugian dari Kisi Terhampar
Penggunaan kisi terhampar kritis dalam pengembangan algoritma SIMPLE. Namun mengadopsi susunan kisi terhampar memiliki kelemahan. Seperti yang disebutkan di atas, dalam dua dan tiga dimensi, diperlukan tiga dan empat sistem kisi terhampar, berturut-turut, dengan komponen kecepatan terintegrasi di atas elemen yang berbeda, seperti yang ditunjukkan dalam Gambar 15.5 untuk situasi dua dimensi.
Selain kebutuhan memori untuk menyimpan sistem kisi untuk setiap komponen kecepatan dan sistem kisi untuk tekanan dan variabel lainnya, prosedur pengeretan itu sendiri menjadi masalah untuk kisi non-Cartesian dan lebih lagi untuk kisi tak terstruktur.
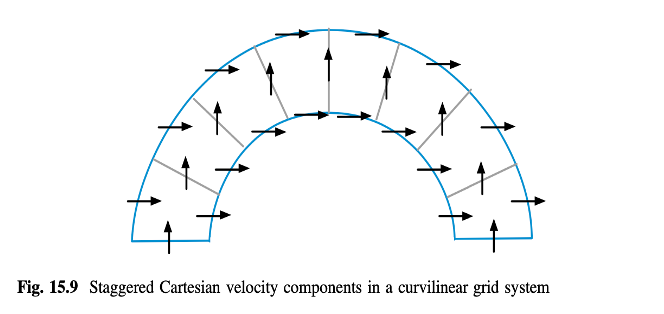
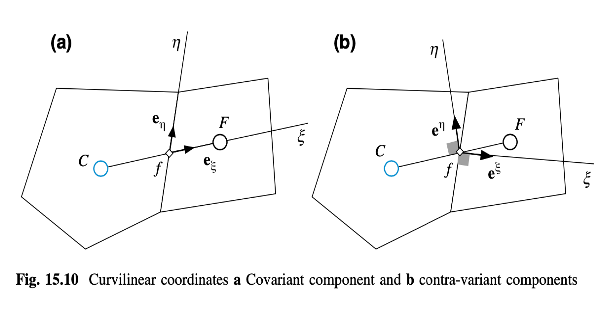
Pada kisi kurvilinear, penggunaan komponen kecepatan Cartesius dapat menyebabkan masalah ketika satu atau lebih permukaan sejajar dengan komponen kecepatan terhampar seperti yang ditunjukkan dalam Gambar 15.9. Oleh karena itu, alternatif yang lebih baik dalam hal ini adalah menggunakan komponen kecepatan kurvilinear kovarian atau kontravarian, seperti yang ditunjukkan dalam Gambar 15.10a, b, masing-masing. Sebuah contoh pengeretan menggunakan komponen kecepatan kontravarian ditunjukkan dalam Gambar (15.11).
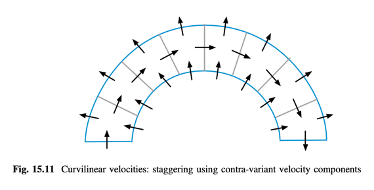
Sayangnya, komplikasi muncul saat mendiskritisasi persamaan momentum dalam koordinat kurvilinear, karena peningkatan kompleksitas dalam penanganan istilah difusi, dan karena persamaan mendapatkan istilah non-konservatif.
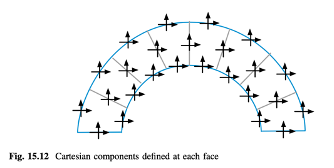
Pilihan lain yang ditunjukkan dalam Gambar 15.12 adalah dengan mengeret semua komponen kecepatan Cartesius dalam semua arah sehingga memiliki semua komponen kecepatan di semua wajah. Ini akan menggandakan (dalam dua dimensi) atau melipatgandakan (dalam tiga dimensi) jumlah persamaan momentum yang harus dipecahkan. Masalahnya menjadi lebih rumit dalam kasus kisi tak terstruktur. Dalam hal ini, tidak ada arah pengeletakan yang jelas, dan satu-satunya cara agar konsep pengeletakan berlaku adalah dengan mengubah ukuran elemen sel yang digunakan untuk komponen tekanan dan kecepatan, atau dengan kembali ke pengeletakan semua komponen kecepatan di sepanjang semua wajah, sekali lagi secara dramatis meningkatkan jumlah variabel yang harus dipecahkan. Akhirnya, informasi geometris yang disimpan lebih dari sekadar dua kali lipat, karena kisi tak terstruktur baru harus digunakan untuk komponen kecepatan.
Ternyata penggunaan sistem kisi terpusat sel terhampar (Gambar 15.13), di mana semua variabel disimpan di lokasi yang sama (pusat sel), adalah solusi yang lebih menarik. Penting untuk dicatat bahwa sementara komponen kecepatan disimpan di pusat elemen seperti halnya untuk tekanan atau variabel lainnya, aliran massa, sebuah nilai skalar, dalam kisi terpusat sel disimpan di wajah elemen. Aliran massa sebenarnya dapat dilihat sebagai komponen kontravarian, kecuali bahwa dalam hal ini dihitung menggunakan interpolasi kustom dari persamaan momentum diskrit, yang dikenal sebagai interpolasi Rhie-Chow, yang menjadi subjek dari bagian berikutnya.

