Kerugian Kecil
Seperti yang dibahas dalam bagian sebelumnya, kehilangan kepala di bagian pipa lurus panjang, yang disebut sebagai kehilangan utama, dapat dihitung dengan menggunakan faktor gesekan yang diperoleh dari baik grafik Moody maupun persamaan Colebrook. Namun, sebagian besar sistem pipa terdiri dari lebih dari pipa lurus. Komponen tambahan tersebut (seperti katup, tikungan, te, dan sejenisnya) menambahkan kehilangan kepala keseluruhan dari sistem. Kehilangan semacam itu umumnya disebut sebagai kehilangan minor, dengan kehilangan kepala yang sesuai disebut sebagai hL minor. Dalam bagian ini kami akan menunjukkan bagaimana cara menentukan berbagai kehilangan minor yang umum terjadi dalam sistem pipa.
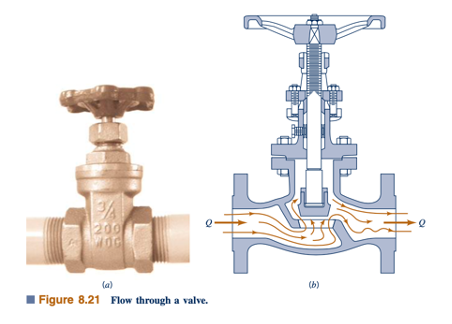
Kehilangan kepala yang terkait dengan aliran melalui sebuah katup adalah kehilangan minor umum. Tujuan dari sebuah katup adalah untuk memberikan cara untuk mengatur laju aliran. Hal ini dicapai dengan mengubah geometri sistem (misalnya, menutup atau membuka katup mengubah pola aliran melalui katup), yang pada gilirannya mengubah kehilangan yang terkait dengan aliran melalui katup. Resistensi aliran atau kehilangan kepala melalui katup bisa menjadi bagian yang signifikan dari resistensi dalam sistem. Bahkan, dengan katup tertutup, resistensi terhadap aliran adalah tak terhingga—fluida tidak dapat mengalir. Kehilangan minor seperti itu mungkin sangat penting. Dengan katup terbuka lebar, resistensi tambahan karena keberadaan katup bisa jadi dapat diabaikan atau tidak.
Pola aliran melalui komponen khas seperti katup ditunjukkan dalam Gambar 8.21. Tidak sulit untuk menyadari bahwa analisis teoritis untuk memprediksi detail aliran seperti ini untuk mendapatkan kehilangan kepala untuk komponen-komponen ini belum, sampai saat ini, memungkinkan. Oleh karena itu, informasi kehilangan kepala untuk hampir semua komponen diberikan dalam bentuk tak berdimensi dan berdasarkan data eksperimental. Metode paling umum yang digunakan untuk menentukan kehilangan kepala atau penurunan tekanan ini adalah dengan menspesifikasikan koefisien kehilangan, KL, yang didefinisikan sebagai

sehingga
Atau
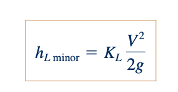
Penurunan tekanan melintasi sebuah komponen yang memiliki koefisien kehilangan KL = 1 sama dengan tekanan dinamis, pV2/2. Seperti yang ditunjukkan oleh Persamaan 8.36 dan gambar di sisi, untuk nilai KL tertentu, kehilangan kepala berbanding lurus dengan kuadrat kecepatan.
Nilai sebenarnya dari KL sangat bergantung pada geometri dari komponen yang dipertimbangkan. Ini juga mungkin tergantung pada sifat-sifat fluida. Artinya,


di mana Re = 𝜌𝑉𝐷/𝜇 adalah jumlah Reynolds pipa. Untuk banyak aplikasi praktis, jumlah Reynolds cukup besar sehingga aliran melalui komponen didominasi oleh efek inersia, dengan efek viskositas menjadi kurang penting. Hal ini terjadi karena percepatan dan perlambatan yang relatif besar yang dialami oleh fluida saat mengalir di sepanjang jalur komponen yang agak melengkung dan berubah-ubah area (bahkan mungkin berliku) (lihat Gambar 8.212). Dalam aliran yang didominasi oleh efek inersia daripada efek viskositas, biasanya ditemukan bahwa penurunan tekanan dan kehilangan kepala berkorelasi langsung dengan tekanan dinamis. Inilah sebabnya mengapa faktor gesekan untuk aliran pipa yang memiliki jumlah Reynolds sangat besar dan sudah berkembang sepenuhnya tidak bergantung pada jumlah Reynolds. Kondisi yang sama juga ditemukan untuk aliran melalui komponen pipa. Dengan demikian, dalam kebanyakan kasus yang menarik secara praktis, koefisien kerugian untuk komponen adalah fungsi dari geometri saja, KL= 𝜙 (geometri).
Kehilangan kecil kadang-kadang diberikan dalam bentuk panjang setara, ℓeq. Dalam terminologi ini, kehilangan kepala melalui komponen diberikan dalam bentuk panjang setara pipa yang akan menghasilkan kehilangan kepala yang sama dengan komponen tersebut. Artinya,
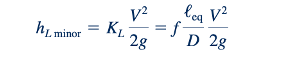
Atau
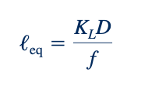
dimana D dan f didasarkan pada pipa yang berisi komponen. Hilangnya head sistem pipa sama dengan kerugian head yang dihasilkan pada pipa lurus yang panjangnya sama dengan pipa-pipa sistem asli ditambah jumlah panjang ekuivalen tambahan seluruh komponen sistem. Kebanyakan analisis aliran pipa, termasuk yang ada dalam buku ini, menggunakan metode koefisien kerugian dibandingkan metode panjang ekuivalen untuk menentukan kerugian kecil.
Banyak sistem pipa mengandung berbagai bagian transisi di mana diameter pipa berubah dari satu ukuran ke ukuran lainnya. Perubahan semacam itu dapat terjadi secara tiba-tiba atau cukup halus melalui beberapa jenis bagian perubahan area. Setiap perubahan dalam area aliran berkontribusi terhadap kerugian yang tidak diperhitungkan dalam perhitungan kehilangan kepala yang sepenuhnya terbentuk (faktor gesekan). Kasus ekstrem melibatkan aliran ke dalam pipa dari wadah (masuk) atau keluar dari pipa ke wadah (keluar).
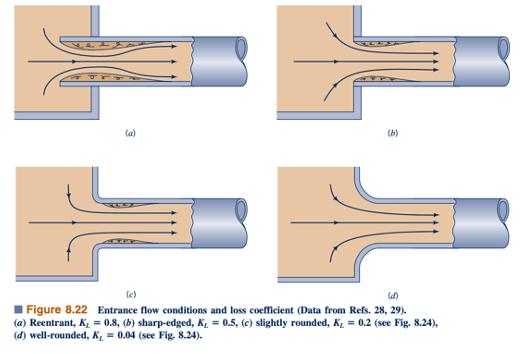
Sebuah fluida dapat mengalir dari wadah ke dalam pipa melalui berbagai bentuk daerah masuk seperti yang digambarkan dalam Gambar 8.22. Setiap geometri memiliki koefisien kerugian yang terkait. Pola aliran tipikal untuk aliran masuk ke pipa melalui pintu masuk dengan pinggiran persegi digambarkan dalam Gambar 8.23. Seperti yang dibahas dalam Bab 3, suatu daerah vena contracta dapat terjadi karena fluida tidak dapat menyelesaikan sudut tajam seketika. Aliran dikatakan terpisah dari sudut tajam tersebut. Kecepatan maksimum di bagian (2) lebih besar dari pada di pipa di bagian (3), dan tekanannya lebih rendah. Jika fluida berkecepatan tinggi ini dapat melambat dengan efisien, energi kinetiknya dapat diubah menjadi tekanan (efek Bernoulli), dan distribusi tekanan ideal yang ditunjukkan dalam Gambar 8.23 akan terjadi. Kehilangan kepala untuk masuk akan menjadi praktis nol.
Hal ini tidak terjadi. Meskipun sebuah fluida dapat dipercepat dengan sangat efisien, sangat sulit untuk memperlambat (decelerate) fluida dengan efisien. Dengan demikian, sebagian energi kinetik tambahan fluida di bagian (2) hilang sebagian karena dissipasi viskos, sehingga tekanannya tidak kembali ke nilai ideal. Kehilangan kepala masuk (penurunan tekanan) diproduksi seperti yang ditunjukkan dalam Gambar 8.23. Sebagian besar kehilangan ini disebabkan oleh efek inersia yang akhirnya terdissipasi oleh tegangan gesek dalam fluida. Hanya sebagian kecil dari kehilangan disebabkan oleh tegangan gesek dinding di dalam daerah masuk. Efek bersihnya adalah bahwa koefisien kerugian untuk masuk berbentuk persegi adalah sekitar KL = 0,50. Setengah dari kepala kecepatan hilang saat fluida masuk ke pipa. Jika pipa menonjol ke dalam tangki (masuk ulang) seperti yang ditunjukkan dalam Gambar 8.22a, kerugian akan lebih besar.
Cara yang jelas untuk mengurangi kehilangan masuk adalah dengan melengkungkan daerah masuk seperti yang ditunjukkan dalam Gambar 8.22c, sehingga mengurangi atau menghilangkan efek vena contracta. Nilai tipikal untuk koefisien kerugian untuk pintu masuk dengan berbagai jumlah pelengkungan bibir ditunjukkan dalam Gambar 8.24. Pengurangan yang signifikan dalam KL dapat diperoleh dengan pelengkungan yang hanya sedikit.

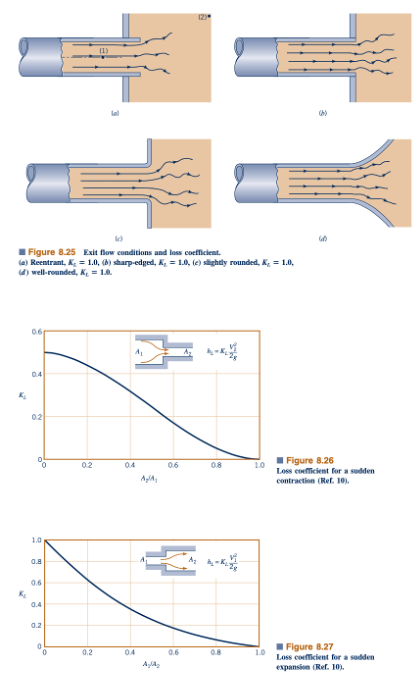
Kehilangan kepala (kerugian keluar) juga terjadi ketika fluida mengalir keluar dari pipa ke dalam sebuah tangki seperti yang ditunjukkan dalam Gambar 8.25. Dalam kasus-kasus ini, energi kinetik seluruh fluida yang keluar (kecepatan V1^2) terdissipasi melalui efek viskos saat aliran fluida bercampur dengan fluida di tangki dan akhirnya berhenti (V2 = 0). Kerugian keluar dari titik (1) dan (2) oleh karena itu setara dengan satu kepala kecepatan, atau KL = 1.
Kerugian juga terjadi karena perubahan diameter pipa seperti yang ditunjukkan dalam Gambar 8.26 dan 8.27. Aliran masuk dan keluar dengan tepi tajam yang dibahas pada paragraf sebelumnya adalah kasus terbatas dari jenis aliran ini dengan A1/A2= ∞, atau A1/ A2 = 0, secara berturut-turut. Koefisien kerugian untuk kontraksi tiba-tiba, KL = hL/ (V^2/2g), adalah fungsi dari rasio area, A2/A1, seperti yang ditunjukkan dalam Gambar 8.26. Nilai KL berubah secara bertahap dari satu ekstrem pintu masuk dengan tepi tajam (A2/A1 = 0 dengan KL ≈ 0,502) ke ekstrem lain tanpa perubahan area (A2/A1=1 dengan KL=0).
Banyak cara, aliran dalam ekspansi tiba-tiba mirip dengan aliran keluar. Seperti yang ditunjukkan dalam Gambar 8.28, fluida meninggalkan pipa yang lebih kecil dan awalnya membentuk struktur seperti jet saat memasuki pipa yang lebih besar. Dalam beberapa diameter di sebelah hilir ekspansi, jet tersebar di seluruh pipa, dan aliran yang sepenuhnya berkembang kembali terbentuk. Dalam proses ini [antara bagian (2) dan (3)], sebagian energi kinetik fluida terdispersi sebagai hasil dari efek viskos. Keluaran berujung persegi adalah kasus terbatas dengan A1/A2 = 0.
Ekspansi tiba-tiba adalah salah satu dari sedikit komponen [mungkin satu-satunya] di mana koefisien kerugian dapat diperoleh dengan analisis sederhana. Untuk melakukan ini, kita pertimbangkan kesinambungan.
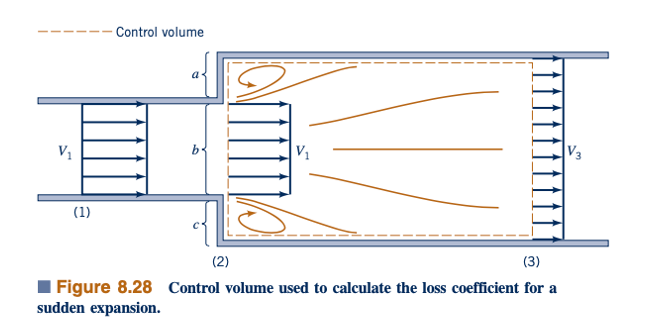
dan persamaan momentum untuk volume kontrol yang ditunjukkan dalam Gambar 8.28 dan persamaan energi diterapkan antara (2) dan (3). Kita asumsikan bahwa aliran seragam di bagian (1), (2), dan (3) dan tekanan konstan di sepanjang sisi kiri volume kontrol (pa= pb= pc= p1). Tiga persamaan pengaturan yang dihasilkan (massa, momentum, dan energi) adalah

Dan
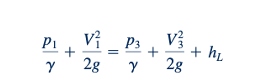
Ini dapat diubah menjadi koefisien rugi, KL=hL(V2'1/2g), seperti:
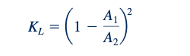
di mana kami telah menggunakan fakta bahwa A2 ≥ A3 . Hasil ini, digambarkan pada Gambar 8.27, sesuai dengan data eksperimental dengan baik. Seperti halnya banyak situasi kerugian kecil lainnya, bukanlah efek viskositas secara langsung (yaitu, tekanan geser dinding) yang menyebabkan kerugian. Sebaliknya, itu adalah dissipasi energi kinetik (jenis efek viskositas lainnya) saat fluida mendekelerasi dengan tidak efisien.
Kerugian mungkin sangat berbeda jika kontraksi atau ekspansi bersifat gradual. Hasil tipikal untuk difuser kerucut dengan rasio area tertentu, A1/A2 , ditunjukkan dalam Gambar 8.29. Difuser adalah perangkat yang dirancang untuk mendekelerasi fluida. Sudut yang dimasukkan dari difuser, u, adalah parameter yang sangat penting. Untuk sudut yang sangat kecil, difuser terlalu panjang dan sebagian besar kerugian kepala disebabkan oleh tekanan geser dinding seperti dalam aliran yang sepenuhnya terembus. Untuk sudut moderat atau besar, aliran terpisah dari dinding dan kerugian terutama disebabkan oleh dissipasi energi kinetik dari jet yang meninggalkan pipa diameter lebih kecil. Bahkan, untuk nilai u yang moderat atau besar (yaitu, u≥35∘ untuk kasus yang,

Seperti yang ditunjukkan pada Gambar 8.29, difuser kerucut, mungkin tidak seperti yang diharapkan, kurang efisien dibandingkan dengan ekspansi dengan tepi tajam yang memiliki KL= (1−A1/A2)'2 . Terdapat sudut optimum u (untuk kasus yang diilustrasikan) di mana koefisien kerugian mencapai minimum. Nilai u yang relatif kecil untuk nilai minimum KL menghasilkan difuser yang panjang, yang menunjukkan bahwa sulit untuk mendekelerasikan fluida dengan efisien.
Perlu dicatat bahwa kondisi yang ditunjukkan pada Gambar 8.29 hanya merupakan hasil yang khas. Aliran melalui difuser sangat kompleks dan mungkin sangat tergantung pada rasio area A2/A1 , detail spesifik geometri, dan nomor Reynolds. Data sering disajikan dalam bentuk koefisien pemulihan tekanan, Cp =(p2-p1) ρV2'1 , yang merupakan rasio kenaikan tekanan statis melintasi difuser terhadap tekanan dinamis masukan. Upaya besar telah dilakukan untuk memahami topik penting ini.
Aliran dalam kontraksi kerucut (nozel; arah aliran terbalik seperti yang ditunjukkan pada Gambar 8.29) kurang kompleks daripada aliran dalam ekspansi kerucut. Koefisien kerugian khas berdasarkan kecepatan downstream (kecepatan tinggi) dapat sangat kecil, berkisar dari KL =0.02 untuk 𝜃 ≥ 30∘ , hingga KL =0.07 untuk 𝜃 ≥ 60∘ , misalnya. Relatif mudah untuk mendekelerasikan fluida dengan efisien.
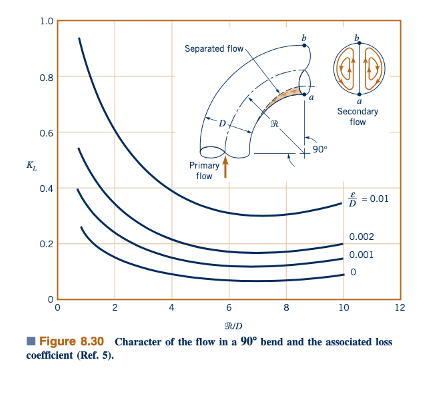
Belokan dalam pipa menghasilkan kerugian kepala yang lebih besar daripada jika pipa tersebut lurus. Kerugian tersebut disebabkan oleh wilayah aliran yang terpisah di dekat bagian dalam belokan (terutama jika belokannya tajam) dan aliran sekunder yang berputar karena ketidakseimbangan gaya sentripetal akibat lengkungan jalur tengah pipa. Efek-efek ini dan nilai-nilai yang terkait dengan KL untuk aliran nomor Reynolds besar melalui belokan 90∘ ditunjukkan pada Gambar 8.30. Kerugian gesekan akibat panjang aksial belokan pipa harus dihitung dan ditambahkan ke kerugian yang diberikan oleh koefisien kerugian pada Gambar 8.30.
Untuk situasi di mana ruang terbatas, perubahan arah aliran sering kali dilakukan dengan menggunakan belokan miter, seperti yang ditunjukkan pada Gambar 8.31, daripada belokan halus. Kerugian yang cukup besar dalam belokan semacam itu dapat dikurangi dengan menggunakan baling-baling panduan yang dirancang dengan cermat untuk membantu mengarahkan aliran dengan lebih sedikit pusaran dan gangguan.
Kategori penting lainnya dari komponen sistem pipa adalah yang terdiri dari fitting pipa yang tersedia secara komersial seperti siku, tee, reducer, katup, dan filter. Nilai-nilai KL untuk komponen-komponen seperti itu sangat bergantung pada bentuk komponen dan hanya sangat lemah tergantung pada nomor Reynolds untuk aliran Re yang besar yang tipikal. Oleh karena itu, koefisien kerugian untuk siku 90° bergantung pada apakah sambungan pipa diulir atau dilas tetapi, dalam akurasi data, cukup independen dari diameter pipa, laju aliran, atau sifat fluida (efek nomor Reynolds). Nilai-nilai tipikal KL untuk komponen-komponen tersebut diberikan dalam Tabel 8.2. Komponen-komponen tipikal ini dirancang lebih untuk kemudahan pembuatan dan biaya daripada untuk mengurangi kerugian kepala yang mereka hasilkan. Laju aliran dari keran di rumah tipikal sudah cukup apakah nilai K untuk sebuah siku adalah K = 1.5 atau dikurangi menjadi K=0.2 dengan menggunakan lengkungan bertahap jari-jari panjang yang lebih mahal.


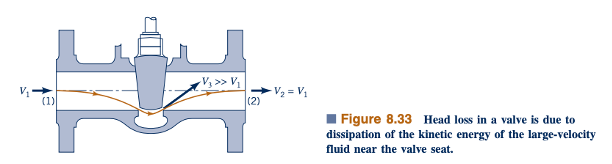
Katup mengendalikan laju aliran dengan memberikan cara untuk menyesuaikan koefisien kerugian sistem secara keseluruhan menjadi nilai yang diinginkan. Ketika katup ditutup, nilai KL adalah tak terhingga dan tidak ada fluida yang mengalir. Ketika katup dibuka, nilai KL berkurang, menghasilkan laju aliran yang diinginkan. Perlu dicatat bahwa koefisien kerugian untuk katup-katup tipikal diberikan dalam Tabel 8.2. Seperti halnya dengan banyak komponen sistem lainnya, kerugian kepala pada katup utamanya disebabkan oleh disipasi energi kinetik dari bagian aliran dengan kecepatan tinggi. Kecepatan tinggi, V3 , diilustrasikan dalam Gambar 8.33.
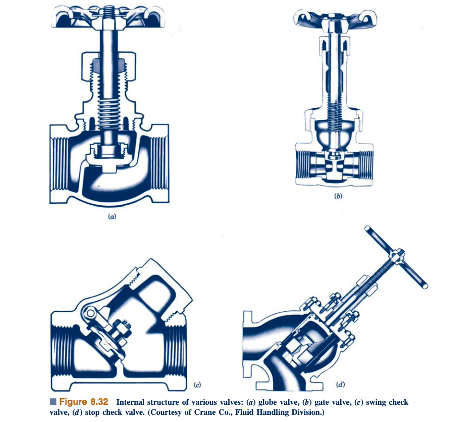
Pembukaan katup mengurangi KL , sehingga menghasilkan laju aliran yang diinginkan. Penampang lintang tipikal dari berbagai jenis katup ditunjukkan dalam Gambar 8.32. Beberapa katup (seperti katup globe konvensional) dirancang untuk penggunaan umum, menyediakan kontrol yang nyaman antara ekstrim secara penuh tertutup dan sepenuhnya terbuka. Lainnya (seperti katup jarum) dirancang untuk memberikan kontrol yang sangat halus terhadap laju aliran. Katup pemeriksa menyediakan operasi tipe dioda yang memungkinkan fluida mengalir hanya ke satu arah.