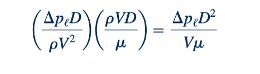Keunikan Istilah Pi
Keunikan istilah Pi. Jika kita merenungkan sedikit tentang proses yang digunakan untuk menentukan pi terms dengan metode variabel berulang, kita akan menyadari bahwa pi terms spesifik yang diperoleh bergantung pada pemilihan variabel berulang yang agak sembarang. Sebagai contoh, dalam masalah mempelajari penurunan tekanan dalam pipa, kita memilih D, V, dan r sebagai variabel berulang. Hal ini mengarah pada formulasi masalah dalam bentuk pi terms sebagai berikut:
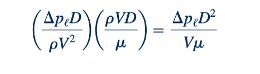
Jika kita memilih D, V, dan m sebagai variabel berulang, maka pi term yang melibatkan ∇𝜌ℓ akan menjadi:
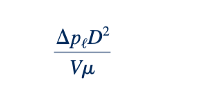
dan pi term kedua tetap sama. Dengan demikian, kita dapat mengekspresikan hasil akhir sebagai:
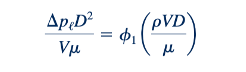

Kedua hasil tersebut benar, dan keduanya akan menghasilkan persamaan akhir yang sama untuk ∇𝜌ℓ. Namun, perlu diperhatikan bahwa fungsi 𝜙 dan 𝜙1 dalam Persamaan 7.5 dan 7.6 akan berbeda karena pi term yang bergantung berbeda untuk kedua hubungan tersebut. Seperti yang ditunjukkan oleh gambar di samping, grafik hasil data tanpa dimensi akan berbeda untuk kedua formulasi tersebut. Namun, ketika mengekstraksi variabel fisik, ∇𝜌ℓ, dari kedua hasil tersebut, nilainya akan sama.
Dari ilustrasi ini, dapat disimpulkan bahwa tidak ada set pi term yang unik yang muncul dari analisis dimensional. Namun, jumlah pi term yang diperlukan tetap, dan setelah set yang benar ditentukan, semua set yang mungkin lainnya dapat dikembangkan dari set ini dengan kombinasi produk dari kekuatan set asli. Dengan demikian, jika kita memiliki masalah yang melibatkan, katakanlah, tiga pi term,
kita selalu bisa membentuk set baru dari yang ada dengan menggabungkan pi term tersebut. Sebagai contoh, kita bisa membentuk pi term baru, Π'2, dengan membiarkan

di mana a dan b adalah eksponen sembarang. Kemudian hubungannya dapat diungkapkan sebagai

Atau
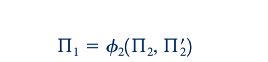
Semuanya akan benar. Namun, perlu ditekankan bahwa jumlah pi term yang diperlukan tidak dapat dikurangi dengan manipulasi ini; hanya bentuk pi term yang berubah. Dengan menggunakan teknik ini, kita dapat melihat bahwa pi terms dalam Persamaan 7.6 bisa diperoleh dari pi terms dalam Persamaan 7.5; yaitu, kita mengalikan ß1 dalam Persamaan 7.5 dengan ß2 sehingga