KONDISI BATAS DINDING
Kondisi batas dinding. Secara umum, kondisi batas no-slip atau slip dapat diterapkan pada dinding yang bergerak atau diam. Implementasinya melibatkan perhitungan dan linearisasi tegangan geser di dinding. Ini berbeda dari kondisi Dirichlet, meskipun untuk grid kartesian, kedua kondisi tersebut dapat ditunjukkan identik.
Kondisi Batas Dinding No-Slip (𝑝𝑏= ?;𝑚𝑏=0 ;𝑉𝑏=𝑉𝑑𝑖𝑛𝑑𝑖𝑛𝑔)
Kondisi batas no-slip mengimplikasikan bahwa kecepatan fluida di dinding vb sama dengan kecepatan dinding vdinding. Untuk dinding diam, kecepatan batas vb adalah nol. Kecepatan yang diketahui di dinding bisa keliru dianggap sebagai kondisi batas Dirichlet. Namun, ini sebenarnya tidak benar, karena yang diperlukan adalah memiliki fluks batas normal nol sambil juga memperhitungkan tegangan geser. Hal ini tidak dapat dipenuhi dengan hanya mengatur = dinding vb=v dinding. Gambar 15.19 menunjukkan bahwa hal ini dapat dijamin dengan memastikan tegangan geser yang tegak lurus terhadap dinding ditambah dengan persamaan kecepatan batas yang sama dengan kecepatan dinding. Gaya Fb yang diberikan oleh dinding pada fluida dapat dituliskan sebagai

di mana 𝐹∥ adalah dalam arah tangensial ke dinding dan 𝐹⊥ adalah dalam arah normal, yang seharusnya nol. Dengan demikian,
di mana τdinding adalah tegangan geser yang diberikan oleh dinding pada fluida yang diberikan oleh
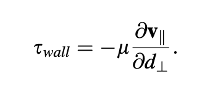
Dalam Persamaan (15.119), 𝑣∥ adalah vektor kecepatan sejajar dengan dinding dan 𝑑⊥ jarak normal dari pusat massa elemen batas ke dinding yang dihitung sebagai

dan n adalah vektor satuan normal dinding. Vektor kecepatan 𝑣∥ dapat dituliskan sebagai selisih antara v dan komponen normalnya seperti

Dari Persamaan (15.119), tegangan geser dinding dapat diaproksimasi menggunakan

dari mana gaya batas untuk aliran laminar dapat diperoleh sebagai

Menggunakan Persamaan (15.123), koefisien elemen batas untuk persamaan momentum dalam arah x, y, dan z dimodifikasi sebagai berikut: persamaan komponen u

Persamaan komponen v

Persamaan komponen w

Tekanan batas yang tidak diketahui pb diekstrapolasi dari solusi interior menggunakan ekspansi deret Taylor yang dipotong di sekitar titik C sehingga tekanan ditemukan dari
atau laju aliran massa diekspresikan melalui interpolasi Rhie-Chow sebagai
Karena laju aliran massa dan kecepatan di batas dinding adalah nol, persamaan di atas menyederhanakan menjadi
yang dapat dimodifikasi menjadi

Mengekspresikan S'b sebagai jumlah dari dua vektor Eb dan Tb, Persamaan (15.130) menjadi
Karena Eb dalam arah Cb, persamaan di atas dapat dimodifikasi menjadi
dari mana tekanan batas diperoleh sebagai


Kondisi Batas Dinding Slip: (pb=?;mb=0; Fb=0)
Untuk kondisi batas ini, tegangan geser dinding adalah nol (Gambar 15.20). Oleh karena itu gaya batas adalah nol. Tekanan batas dihitung seperti kasus dinding no-slip menggunakan Persamaan (15.127) atau Persamaan (15.133). Koefisien persamaan momentum (dalam bentuk vektor) dimodifikasi sebagai berikut:

