konservasi momentum

Hukum Konservasi Momentum
- Hukum konservasi momentum dapat dinyatakan sebagai berikut;
- Dimana b ini mewakili gaya badan (body force) per satuan massa. Gaya badan mewakili segala gaya yang tidak bekerja pada permukaan batas, termasuk yang bekerja dari jarak jauh, seperti gaya gravitasi.
- Persamaan ini diperoleh dengan mempertimbangkan laju perubahan momentum dari sejumlah partikel massa. Mempertimbangkan suatu volume bahan dengan massa tetap yang bergerak melalui ruang, dan karenanya laju diungkapkan melalui turunan material
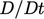 .
.
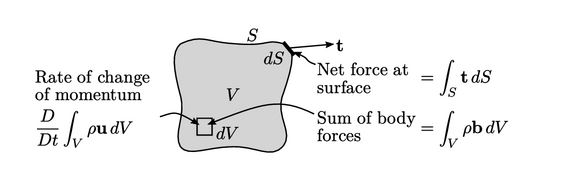
- Menerapkan Teorema Gauss dan Persamaan (2.16), gaya permukaan adalah
- Menyamakan laju perubahan momentum dengan gaya dan, memperhatikan massa tetap sehingga
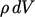 persamaan konstan dalam waktu, menghasilkan persamaan
persamaan konstan dalam waktu, menghasilkan persamaan
- Integralnya harus sama dengan 0, menghasilkan Persamaan (2.19).
- Divergensi dijelaskan dalam bagian 2.4 sebagai fluks melintasi suatu permukaan per satuan volume sebagai persamaan
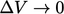 . Divergensi tegangan juga mewakili fluks tegangan melintasi permukaan, yaitu gaya per satuan volume sebagai persamaan
. Divergensi tegangan juga mewakili fluks tegangan melintasi permukaan, yaitu gaya per satuan volume sebagai persamaan 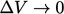 , diberikan oleh
, diberikan oleh
- Persamaan (2.19) secara khusus terkait dengan momentum linear. Sebagai gantinya, konservasi momentum sudut, dalam ketiadaan “tegangan kopel” yang menghasilkan medan momen, diberikan oleh
- Turunan Persamaan (2.23) cukup kompleks sehingga dihilangkan di sini.
Tensor Symmetry
- Simetri dalam suatu persamaan tensor T mengacu pada komponen-komponen yang simetris terhadap diagonal, yaitu
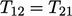 ,
, 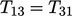 dan
dan 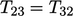 . Tranposisi dari sebuah tensor, ditandai dengan superskrip T, menukar komponen- komponen melintasi diagonal seperti berikut
. Tranposisi dari sebuah tensor, ditandai dengan superskrip T, menukar komponen- komponen melintasi diagonal seperti berikut
- Maka, sebuah tensor T simetris jika
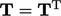 . Sebuah tensor skew (anti-simetris) memiliki sifat
. Sebuah tensor skew (anti-simetris) memiliki sifat 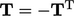 . Sebuah tensor dapat dipecah menjadi bagian simetris dan skew dengan melakukan perhitungan berikut :
. Sebuah tensor dapat dipecah menjadi bagian simetris dan skew dengan melakukan perhitungan berikut :
