konservasi massa
Hukum konservasi massa dapat dinyatakan dengan persamaan berikut:
dimana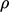 
adalah kerapatan massa. Persamaan ini dapat diperoleh dengan mempertimbangkan suatu volume 
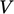yang tetap dalam ruang (perhatikan !!), dibatasi oleh suatu permukaan (S). Jika volume tersebut diisi oleh fluida dengan kerapatan (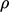), Massa fluida di dalamnya adalah
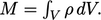
Laju peningkatan massa di dalam volume harus sebanding dengan laju aliran masuk massa melalui permukaan volume tersebut. Yang terakhir ini dihitung dengan mengintegrasikan fluks massa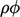 
di atas permukaan, dengan memperhatikan tanda negatif karena (dS) mengarah keluar volume
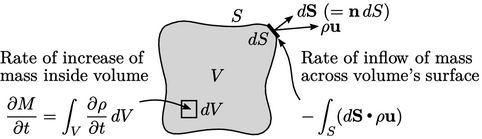
Teorema Gauss menghubungkan integral permukaan dan integral volume dengan persamaan :
Menyamakan laju peningkatan massa dengan laju aliran dan menerapkan persamaan (2.9) didapatkan persamaan sebagai berikut
- Karena integral tersebut berlaku untuk volume (V) apa pun, maka integranya (dalam […]) harus sama dengan 0, yang menghasilkan persamaan (2.8).
Divergence
- Divergensi, yang ditunjukkan oleh
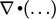, menunjukkan kecenderungan dari medan vector untuk menunjuk ke luar dari suatu permukaan tertutup. Sebagai contoh, ketika divergensi dari kecepatan 
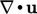positif, fluids tersebut sedang memperluas; divergensi negative menunjukkan kontraksi. Bayangkan suatu volume fluida dengan distribusi kompleks dari (u) pada permukaan batasnya, di bawah kiri. Perhitungan 
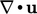akan mengisolasi komponen yang sedang memperluas (kanan) dari aliran seragam (tengah).
- Divergensi dari kecepatan dihitung dengan melakukan integrasi – yaitu, menjumlahkan – fluks-fluks di atas permukaan tertutup. Untuk mendefinisikan divergensi di suatu titik permukaan (S) yang melingkupi suatu volume (
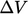), divergensi adalah fluks melintasi permukaan per unit volume, seperti (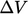), misalnya
Nabla operator
- Symbol nabla
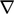dapat dianggap sebagai operator vektor
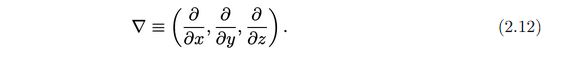
- Divergensi produk (u) dengan nabla (
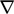), menjadi
