10.2.9 Langkah Substitusi
Setelah mendekomposisi matriks asli A menjadi L dan U, sistem persamaan dapat dipecahkan dalam dua langkah melalui Persamaan (10.18) dan (10.14). Perhatikan bahwa prosedur dua langkah ini setara dengan menyelesaikan dua sistem persamaan linear, tetapi sekarang disederhanakan oleh kenyataan bahwa L dan U berbentuk matriks segitiga bawah dan segitiga atas, masing-masing.
Pada langkah pertama, vektor c diperoleh dari Persamaan (10.18) melalui substitusi maju. Proses ini dapat dijelaskan sebagai
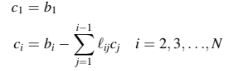
Pada langkah kedua, nilai-nilai ditemukan dari Persamaan (10.14) melalui substitusi mundur. Proses ini dapat dijelaskan sebagai
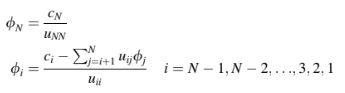
Elemen-elemen dari L dan U dapat langsung disimpan dalam matriks asli A jika tidak lagi diperlukan. Hal ini karena elemen-elemen dari A hanya diperlukan ketika elemen-elemen yang sesuai dari L atau U dihitung. Jumlah operasi yang diperlukan untuk melakukan faktorisasi LU dari matriks persegi berukuran dua kali lipat dari jumlah operasi yang diperlukan untuk menyelesaikan sistem persamaan yang sama dengan eliminasi Gauss. Lagi-lagi, keuntungan menggunakan faktorisasi LU adalah ketika matriks A yang sama berlaku untuk banyak sistem dengan vektor b yang berbeda. Namun, alasan utama untuk memperkenalkan faktorisasi LU adalah karena ini membentuk dasar untuk mengembangkan beberapa solver iteratif yang lebih efisien untuk sistem persamaan linear algebra. Hal ini akan diperkenalkan dalam bagian berikutnya.
