Lapisan batas termal
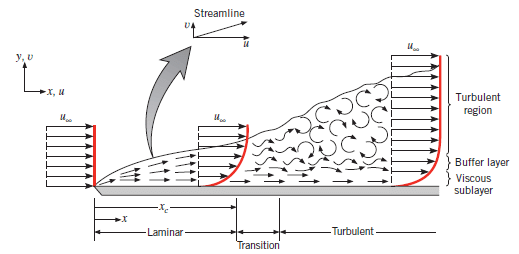
Lapisan Batas Termal. Dalam lapisan batas turbulen, distribusi suhu mirip dengan kecepatan, dengan sub-lapisan kental dan intersial, dipisahkan oleh lapisan penyangga, seperti yang dibahas dalam Bagian. 7.4.
Dengan analogi dengan 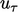 , Persamaan. (7.10), kami mendefinisikan suhu gesekan sebagai
, Persamaan. (7.10), kami mendefinisikan suhu gesekan sebagai
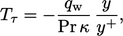 | (7.49) |
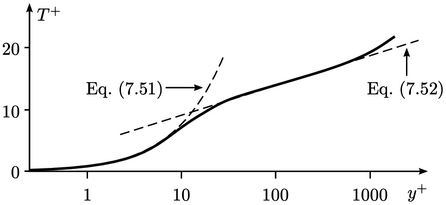
Lapisan dinding kemudian digambarkan dengan suhu yang tidak berdimensi
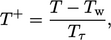 | (7.50) |
di mana 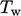 suhu fluida di dinding. Mengabaikan pembentukan panas akibat tegangan viskos, profil pada sub-lapisan viskos digambarkan dengan hubungan
suhu fluida di dinding. Mengabaikan pembentukan panas akibat tegangan viskos, profil pada sub-lapisan viskos digambarkan dengan hubungan
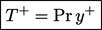 | (7.51) |
Profil pada sub-lapisan inersia biasanya digambarkan dengan hukum log untuk 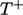
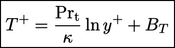 | (7.52) |
Turunan dari Persamaan. (7.51) dan Persamaan. (7.52) mengasumsikan fluks panas konstan melintasi profil, sama dengan 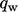 di dinding. Pada sublapisan kental, fluks panas bersifat laminar, jadi
di dinding. Pada sublapisan kental, fluks panas bersifat laminar, jadi 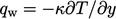 dan
dan
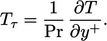 | (7.53) |
Persamaan ini terintegrasi antara 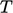 pada jarak
pada jarak 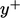 dari dinding ke
dari dinding ke 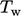 dinding, sehingga menghasilkan Persamaan. (7.51). Pada lapisan inersia, fluks panas diasumsikan turbulen
dinding, sehingga menghasilkan Persamaan. (7.51). Pada lapisan inersia, fluks panas diasumsikan turbulen 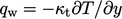 dan
dan
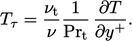 | (7.54) |
Menggabungkan Persamaan. (6.24), Persamaan. (7.9) dan Persamaan. (7.15) menghasilkan rasio 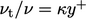 . Mengganti dalam Persamaan. (7.54) dan mengintegrasikan kemudian mengarah ke Persamaan. (7.52) dimana
. Mengganti dalam Persamaan. (7.54) dan mengintegrasikan kemudian mengarah ke Persamaan. (7.52) dimana 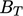 adalah konstanta integrasi.
adalah konstanta integrasi.
Konstanta 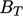 umumnya dianggap sebagai fungsi dari
umumnya dianggap sebagai fungsi dari 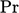 . Perkiraan yang masuk akal untuk fungsi ini adalah20
. Perkiraan yang masuk akal untuk fungsi ini adalah20
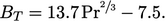 | (7.55) |
Fungsi lain yang biasa digunakan pada fungsi thermal wall adalah 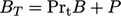 , dimana
, dimana 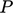 fungsi dari
fungsi dari 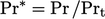 :
:
![h 3=4 i P = 9:24 (Pr ) 1 [1 + 0:28 exp ( 0:007Pr )]: \relax \special {t4ht=](https://doc.cfd.direct/notes/cfd-general-principles/img/index3375x.png) | (7.56) |
Ekspresi untuk 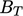 menggunakan koefisien
menggunakan koefisien 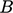 dari Persamaan. (7.11). Konstanta integrasi ini terkadang dimasukkan ke dalam fungsi log sebagai koefisien “
dari Persamaan. (7.11). Konstanta integrasi ini terkadang dimasukkan ke dalam fungsi log sebagai koefisien “ 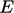 ” dalam ekspresi hukum log, sebagaimana catatan kaki di halaman 483 menjelaskan.
” dalam ekspresi hukum log, sebagaimana catatan kaki di halaman 483 menjelaskan.
