lapisan Turbulent

Lapisan Batas Yang Bergejolak. Pada dinding padat, kecepatan aliran tangensial 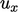 meningkat dengan cepat melintasi lapisan batas tipis, seperti yang dibahas pada Sec. 6.4. Pada kecepatan tinggi
meningkat dengan cepat melintasi lapisan batas tipis, seperti yang dibahas pada Sec. 6.4. Pada kecepatan tinggi 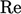 , profil kecepatan mempunyai karakter universal yang ditunjukkan di bawah ini.
, profil kecepatan mempunyai karakter universal yang ditunjukkan di bawah ini.

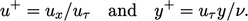 | (7.9) |
Terakhir, pada sublapisan inersia karena 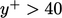 , aliran bersifat turbulen dan profil kecepatan dijelaskan oleh hukum logaritmik dinding , sering disingkat menjadi hukum log saja , menurut
, aliran bersifat turbulen dan profil kecepatan dijelaskan oleh hukum logaritmik dinding , sering disingkat menjadi hukum log saja , menurut
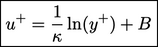 | (7.13) |
Persamaannya mencakup konstanta Kármán 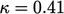 dan konstanta Kármán
dan konstanta Kármán 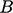 . Untuk dinding yang halus,
. Untuk dinding yang halus,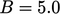 – 5.5 umum digunakan. Kedua Persamaan. (7.11) dan Persamaan. (7.13) dapat diturunkan dengan asumsi tegangan geser konstan pada seluruh profil, sama dengan
– 5.5 umum digunakan. Kedua Persamaan. (7.11) dan Persamaan. (7.13) dapat diturunkan dengan asumsi tegangan geser konstan pada seluruh profil, sama dengan 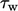 pada dinding. Pada sublapisan kental, tegangan geser bersifat laminar, jadi
pada dinding. Pada sublapisan kental, tegangan geser bersifat laminar, jadi
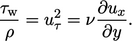 | (7.14) |
Persamaan ini berintegrasi dengan konstanta integrasi nol sehingga menghasilkan 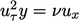 Persamaan. (7.11) diturunkan. Pada sublapisan inersia, tegangan geser bersifat turbulen (laminar dapat diabaikan), jadi
Persamaan. (7.11) diturunkan. Pada sublapisan inersia, tegangan geser bersifat turbulen (laminar dapat diabaikan), jadi
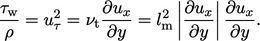 | (7.15) |
Dengan asumsi 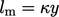 give
give 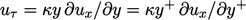 , yang terintegrasi untuk menghasilkan Persamaan. (7.13). Dalam sub-lapisan inersia,
, yang terintegrasi untuk menghasilkan Persamaan. (7.13). Dalam sub-lapisan inersia, 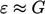 seperti dijelaskan dalam Persamaan. (7.5), yang digabungkan dengan Persamaan. (7.15) dan Persamaan. (6.31) memberi
seperti dijelaskan dalam Persamaan. (7.5), yang digabungkan dengan Persamaan. (7.15) dan Persamaan. (6.31) memberi
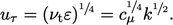 | (7.16) |

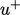
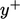
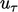 yang berhubungan dengan tegangan geser dinding
yang berhubungan dengan tegangan geser dinding 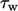 sebesar
sebesar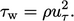
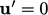 . Dekat dengan dinding,
. Dekat dengan dinding, 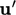 ditekan, menciptakan wilayah dimana alirannya laminar
ditekan, menciptakan wilayah dimana alirannya laminar 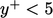 , yang dikenal sebagai
, yang dikenal sebagai 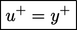
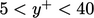 . Van Dried memberikan model peningkatan panjang pencampuran melalui wilayah ini, dengan
. Van Dried memberikan model peningkatan panjang pencampuran melalui wilayah ini, dengan