Limiting Multiple components
Limiting Multiple Components. Perhitungan dan penerapan limiter diperkenalkan di Sec. 3.11 untuk adveksi properti skalar tunggal. Gambar di bawah ini menunjukkan sifat adveksi yang berupa vektor, misalnya 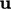 dalam persamaan kekekalan momentum. (2.47).
dalam persamaan kekekalan momentum. (2.47).
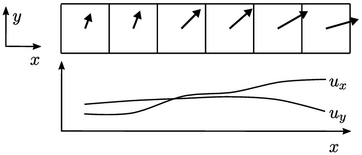
Ini menunjukkan potongan 2D sepanjang bidang 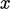 –
– 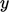 melalui pilihan sel dalam jaring teratur dengan vektor kecepatan
melalui pilihan sel dalam jaring teratur dengan vektor kecepatan 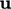 ditampilkan untuk setiap sel. Ketika
ditampilkan untuk setiap sel. Ketika 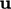 diinterpolasi ke permukaan sepanjang
diinterpolasi ke permukaan sepanjang 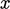 arah – menggunakan skema terbatas, pendekatan paling sederhana adalah dengan menghitung limiter untuk setiap komponen vektor, misalnya
arah – menggunakan skema terbatas, pendekatan paling sederhana adalah dengan menghitung limiter untuk setiap komponen vektor, misalnya 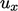 , dan menginterpolasi komponen dengan limiter tersebut.
, dan menginterpolasi komponen dengan limiter tersebut.
Pada contoh di atas, profil dari 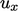 dan
dan 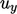 ke
ke 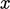 arah – cukup berbeda, sehingga limiter yang dihitung akan berbeda untuk
arah – cukup berbeda, sehingga limiter yang dihitung akan berbeda untuk 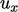 dan
dan 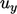 komponen pada masing-masing sisi. Pembatasannya tidak akan invarian pada rotasi sumbu koordinat, sehingga menghasilkan solusi yang berbeda bergantung pada orientasi awal geometri terhadap sumbu.
komponen pada masing-masing sisi. Pembatasannya tidak akan invarian pada rotasi sumbu koordinat, sehingga menghasilkan solusi yang berbeda bergantung pada orientasi awal geometri terhadap sumbu.
Pembatasannya bisa invarian dengan menggunakan pembatas tunggal yang dihitung dari besarannya 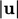 , yang diterapkan pada semua komponen
, yang diterapkan pada semua komponen 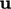 . Kekuatan pembatas berhubungan dengan rata-rata seluruh komponen, yang biasanya tidak mencukupi untuk komponen yang memerlukan pembatas terkuat. Hal ini dapat menyebabkan ketidakstabilan.
. Kekuatan pembatas berhubungan dengan rata-rata seluruh komponen, yang biasanya tidak mencukupi untuk komponen yang memerlukan pembatas terkuat. Hal ini dapat menyebabkan ketidakstabilan.
Sebaliknya, skema ‘V’ menghitung pembatas berdasarkan arah ‘kasus terburuk’, yaitu arah gradien paling curam pada 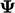 permukaan sel. Ia menggunakan ekspresi berikut untuk
permukaan sel. Ia menggunakan ekspresi berikut untuk  vektor
vektor 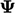 , menggantikan Persamaan. (3.12) untuk skalar:
, menggantikan Persamaan. (3.12) untuk skalar:
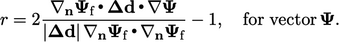 | (3.17) |
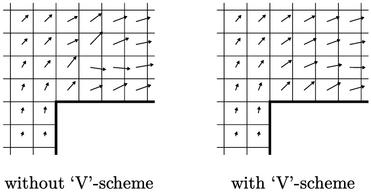
Meskipun skema V memastikan invarian, skema ini juga memberikan stabilitas yang lebih besar daripada pembatasan komponen. Hal ini dapat menghilangkan osilasi dalam larutan, misalnya pada contoh aliran supersonik di atas pada suatu langkah yang menunjukkan pengaruh kecepatan pada sel yang berdekatan dengan sudut langkah.
Pembatasan multivarian
Pembatasan multivariat menerapkan pembatas yang sama untuk diskritisasi adveksi pada himpunan 2 persamaan atau lebih. Ia bekerja dengan menghitung limiter 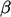 untuk setiap variabel solusi dalam kumpulan persamaan dan menerapkan nilai terendah
untuk setiap variabel solusi dalam kumpulan persamaan dan menerapkan nilai terendah 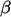 ke semua persamaan.
ke semua persamaan.
Hal ini dapat digunakan untuk menjaga konsistensi dalam pengangkutan spesies fluida individual, seperti 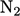 ,
, 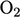 , misalnya dalam perambatan api laminar (yang berada di luar cakupan buku ini).
, misalnya dalam perambatan api laminar (yang berada di luar cakupan buku ini).
