Lompatan Hidraulik
Lompatan Hidraulik. Observasi aliran dalam saluran terbuka menunjukkan bahwa dalam kondisi tertentu, mungkin terjadi perubahan kedalaman cairan dengan sangat cepat dalam jarak pendek saluran tanpa ada perubahan dalam konfigurasi saluran. Perubahan kedalaman seperti itu dapat diaproksimasi sebagai ketidakteraturan dalam elevasi permukaan bebas, dengan turunan spatikal kedalaman (dy/dx) yang besar. Dengan alasan yang dibahas di bawah ini, perubahan kedalaman ini selalu dari kedalaman dangkal menjadi lebih dalam—selalu naik, tidak pernah turun.
Secara fisik, dekat dengan ketidakteraturan, yang disebut lonjakan hidrolik, mungkin terjadi ketika terjadi konflik antara pengaruh hulu dan hilir yang mengontrol suatu bagian tertentu dari saluran. Sebagai contoh, sebuah pintu air mungkin membutuhkan kondisi pada bagian hulu saluran (di hilir pintu air) untuk mengalir secara superkritis, sementara halangan di saluran di ujung hilir dari bagian saluran mungkin memerlukan aliran subkritis. Lonjakan hidrolik memberikan mekanisme (meskipun hampir tidak teratur) untuk melakukan transisi antara dua jenis aliran tersebut.
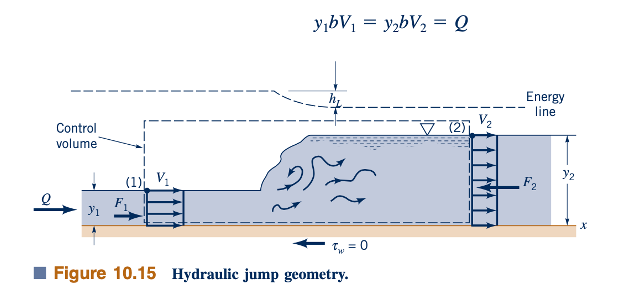
Jenis lonjakan hidrolik yang paling sederhana terjadi dalam saluran horizontal berbentuk persegi panjang seperti yang terindikasi dalam Gambar 10.15. Meskipun aliran dalam lonjakan itu sendiri sangat kompleks dan terganggu, adalah wajar untuk mengasumsikan bahwa aliran di bagian 112 dan 122 hampir seragam, stabil, dan satu dimensi. Selain itu, kita mengabaikan tegangan geser dinding tw, dalam segmen yang relatif pendek antara dua bagian ini. Dalam kondisi ini, komponen x dari persamaan momentum (Eq. 5.22) untuk volume kontrol yang ditunjukkan dapat ditulis sebagai:

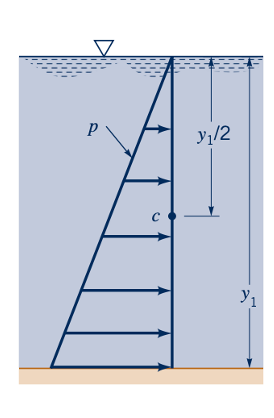
di mana, seperti yang ditunjukkan oleh gambar di margin, gaya tekanan di kedua bagian bersifat hidrostatik. Artinya, F1 =pc1A1 =𝛾y^12/ b2 dan F2 =pc2 A2 =𝛾y^22 /b2, di mana pc1=𝛾y1/2 dan pc2 =𝛾y2/2 adalah tekanan di sentroid penampang saluran dan b adalah lebar saluran (lihat Bagian 2.8). Dengan demikian, persamaan momentum menjadi:

Selain persamaan momentum, kita memiliki persamaan kekekalan massa (Eq. 5.12).
dan persamaan energi (Eq. 5.84).

Kehilangan kepala, hL , dalam Persamaan 10.23 disebabkan oleh pencampuran turbulent yang kuat dan dissipasi yang terjadi dalam lonjakan itu sendiri. Kita telah mengabaikan kehilangan kepala akibat tegangan geser dinding.
Jelas bahwa Persamaan 10.21, 10.22, dan 10.23 memiliki solusi y1 =y2 ,V1 =V2 , dan hL =0. Ini mewakili kasus trivial tanpa lonjakan. Karena ini adalah persamaan nonlinear, mungkin ada lebih dari satu solusi. Solusi lain dapat diperoleh sebagai berikut. Dengan menggabungkan Persamaan 10.21 dan 10.22 untuk menghilangkan V2 kita dapatkan:
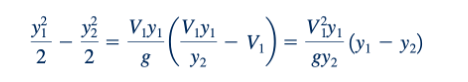
yang dapat disederhanakan dengan mengeluarkan faktor bersama yang tidak nol y1 - y2 dari setiap sisi sehingga menjadi:
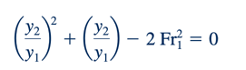
di mana Fr1=V1/ √𝑔𝑦1 adalah Froude number hulu. Dengan menggunakan rumus kuadrat, kita dapatkan:

Jelas bahwa solusi dengan tanda minus tidak mungkin (akan memberikan y2/y1 yang negatif). Oleh karena itu,
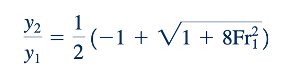
Rasio kedalaman ini, y2 /y1 , melintasi lonjakan hidrolik ditunjukkan sebagai fungsi dari Froude number hulu dalam Gambar 10.16. Bagian kurva untuk Fr1 ≤1 digarisbawahi mengakui bahwa untuk memiliki lonjakan hidrolik aliran harus superkritis. Artinya, solusi sebagaimana yang diberikan oleh Persamaan 10.24 harus dibatasi pada Fr1 >1, di mana y2 /y1 >1. Hal ini dapat ditunjukkan dengan mempertimbangkan persamaan energi, Persamaan 10.23, sebagai berikut. Kehilangan kepala tak berdimensi, hL/y1 , dapat diperoleh dari Persamaan 10.23 sebagai:

di mana, untuk nilai tertentu dari Fr1 , nilai-nilai dari y2 /y1 diperoleh dari Persamaan 10.24. Seperti yang ditunjukkan dalam Gambar 10.16, kehilangan kepala negatif jika Fr1 ≤1. Karena kehilangan kepala negatif melanggar hukum kedua:

efek viskositas mendissipasi energi, mereka tidak dapat menciptakan energi; lihat Bagian 5.32, tidak mungkin untuk menghasilkan lonjakan hidrolik dengan Fr 1 ≤1. Kehilangan kepala melintasi lonjakan ditunjukkan oleh penurunan garis energi seperti yang ditunjukkan dalam Gambar 10.15.
Aliran harus superkritis (Fr > 1 ) untuk menghasilkan diskontinuitas yang disebut lonjakan hidrolik. Ini analog dengan konsep aliran yang dapat dipadatkan yang dibahas dalam Bab 11 di mana ditunjukkan bahwa aliran gas harus supersonik (bilangan Mach > 1 ) untuk menghasilkan diskontinuitas yang disebut gelombang kejut normal. Namun, kenyataan bahwa aliran superkritis (atau supersonik) tidak menjamin produksi lonjakan hidrolik (atau gelombang kejut). Solusi trivial y1 =y2 dan V1 =V2 juga mungkin.
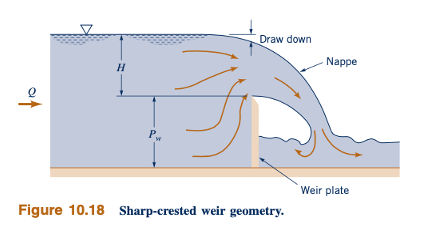
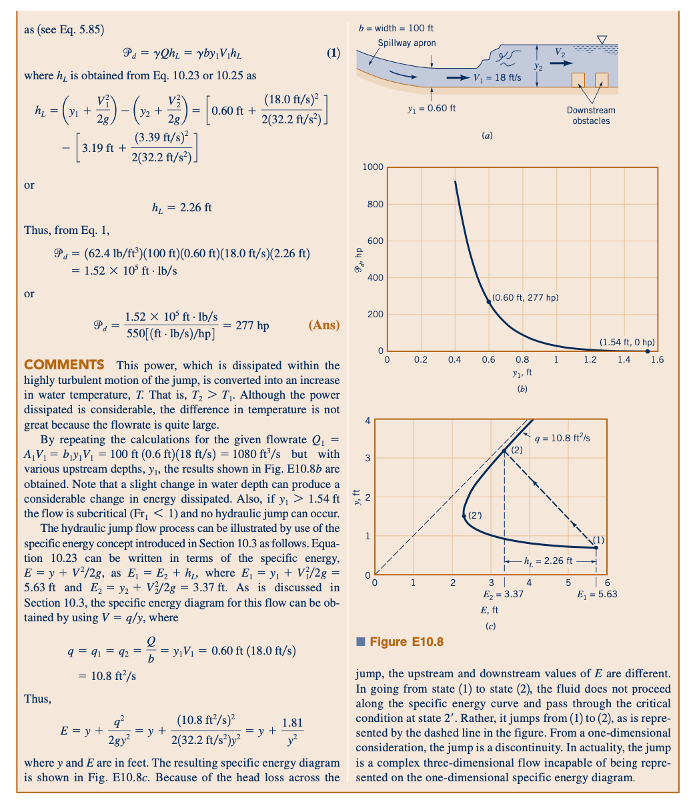
Fakta bahwa terjadi kehilangan energi melintasi lonjakan hidrolik berguna dalam banyak situasi. Sebagai contoh, jumlah energi yang relatif besar yang terkandung dalam fluida yang mengalir di saluran pelimpah bendungan seperti yang ditunjukkan dalam gambar di margin dapat menyebabkan kerusakan pada saluran di bawah bendungan. Dengan menempatkan objek pengendali aliran yang sesuai di saluran hilir dari pelimpah, adalah mungkin (jika aliran bersifat superkritis) untuk menghasilkan lonjakan hidrolik di pelataran pelimpah dan dengan demikian mendispersikan sebagian besar energi aliran. Artinya, pelimpah bendungan menghasilkan aliran superkritis, dan saluran di hilir bendungan memerlukan aliran subkritis. Lonjakan hidrolik yang dihasilkan memberikan cara untuk mengubah karakter aliran.

Struktur sebenarnya dari lonjakan hidrolik adalah fungsi kompleks dari Fr, meskipun rasio kedalaman dan kehilangan kepala diberikan dengan cukup akurat oleh analisis aliran satu dimensi yang sederhana (Eqs. 10.24 dan 10.25). Investigasi detail tentang aliran menunjukkan bahwa pada dasarnya ada lima jenis kondisi permukaan dan lonjakan. Klasifikasi lonjakan ini ditunjukkan dalam Tabel 10.2, beserta sketsa struktur lonjakan. Untuk aliran yang hampir superkritis, lonjakan lebih mirip gelombang berdiri, tanpa perubahan kedalaman yang hampir tiba-tiba. Pada beberapa rentang angka Froude, lonjakan
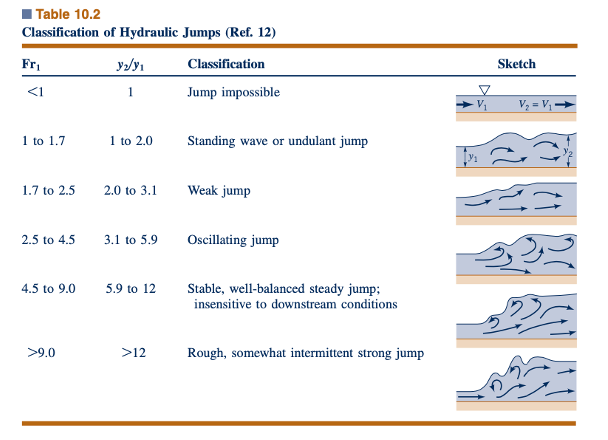
Tidak stabil, dengan osilasi periodik reguler yang bergerak secara teratur ke hilir. (Ingat bahwa gelombang tidak dapat bergerak ke hulu melawan aliran superkritis.)
Lonjakan hidrolik (jarak antara aliran hampir seragam di hulu dan hilir) mungkin penting dalam desain saluran. Meskipun nilainya tidak dapat ditentukan secara teoritis, hasil eksperimen menunjukkan bahwa dalam rentang yang luas dari angka Froude, lonjakan ini kira-kira panjangnya tujuh kedalaman hilir (Ref. 52).
Lonjakan hidrolik dapat terjadi dalam berbagai konfigurasi aliran saluran, bukan hanya dalam saluran horizontal dan berbentuk persegi panjang seperti yang dibahas di atas. Lonjakan dalam saluran non-persegi panjang (misalnya, pipa bulat, kanal trapesium) berperilaku cukup mirip dengan yang dalam saluran persegi panjang, meskipun detail rasio kedalaman dan kehilangan kepala sedikit berbeda dari lonjakan dalam saluran persegi panjang.
Jenis lonjakan hidrolik lainnya termasuk yang terjadi dalam saluran miring, seperti yang ditunjukkan dalam Fig. 10.17a, dan lonjakan hidrolik yang tenggelam yang dapat terjadi tepat di hilir dari