2.3.5 Matriks Simetris Positif Definit
Sebuah matriks simetris berorde N dikatakan positif-definite jika untuk semua vektor kolom p dalam
ketidaksetaraan berikut berlaku:
Sebagai contoh, jika A adalah matriks simetris berorde 3 yang diberikan oleh,
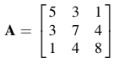
Maka Persamaan (2.50) untuk setiap vektor kolom p berorde 3 memberikan,
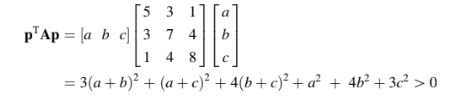
yang bersifat positif-definit. Jika A adalah matriks simetris positif-definit yang diberikan oleh,

Maka, antara lain, berlaku sifat-sifat berikut:
- Setiap sub-matriks P dari A berorde M x (N-M+1) dengan bentuk,

juga positif-definit.
- N eigenvalue dari A, λ1, λ2, λ3,…, λN adalah positif.
- Jika semua eigenvalue dari matriks A adalah positif, maka A adalah positif-definit.
- A memiliki dekomposisi unik dalam bentuk A = LLT, di mana L adalah matriks segitiga bawah. Dekomposisi ini dikenal sebagai dekomposisi Cholesky.
