6.3.3 Mengakses Lapangan Elemen
Mengakses lapangan dalam grid terstruktur sama mudahnya seperti menggunakan indeks elemen. Oleh karena itu, dalam ruang dua dimensi, φ(i,j) atau φi j adalah nilai dari lapangan φ pada elemen (i, j). Seperti yang ditunjukkan dalam Gambar 6.7a, nilai-nilai φ di sel-sel tetangga untuk (i, j) adalah, masing-masing dan
Seperti yang disebutkan di atas, menghitung gradien menggunakan Persamaan (6.4) memerlukan perhitungan nilai φ di setiap wajah volume hingga (untuk elemen semu kita, wajah depan dan belakang memiliki nilai yang sama dan oleh karena itu tidak akan dimasukkan dalam perhitungan). Oleh karena itu, selain nilai φ pada titik (i, j), nilai-nilai φ di titik-titik tetangga (i + 1, j), (i − 1, j), (i, j + 1), dan (i, j − 1) juga diperlukan. Dalam grid terstruktur, informasi ini sudah tersedia dan nilai di wajah dihitung dengan interpolasi sederhana antara nilai φ di pusat massa dua volume yang berbagi wajah. Dengan menggunakan Persamaan (6.5), nilai terinterpolasi di wajah (i +1/2, j) dalam istilah indeks lokal dapat dituliskan sebagai berikut,
Rincian interpolasi linear akan disajikan lebih lanjut dalam bab ini. Mengacu pada Gambar 6.7a, gradien pada elemen (i, j) dapat dihitung menggunakan indeks lokal sebagai berikut
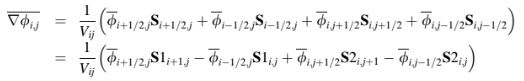
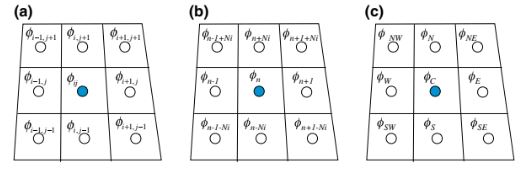
Gambar 6.7 Indeks Lokal versus Indeks Global versus Indeks Diskritisasi. a Indeks Lokal, b Indeks Global, dan c Indeks Diskritisasi
sementara menggunakan sistem indeks global, Gambar 6.7b, menjadi,
Perlu dicatat bahwa S adalah vektor luar yang normal terhadap permukaan di wajah kontrol volume. Kecuali di batas domain, wajah-wajah kontrol volume dibagi oleh dua elemen. Oleh karena itu, arah keluar untuk satu elemen akan mewakili arah masuk untuk elemen lainnya. Oleh karena itu, untuk menghindari penggandaan vektor permukaan di antarmuka, hanya satu vektor yang dihitung dan disimpan di antarmuka; yang mengarah ke arah peningkatan i atau j. Fitur-fitur tertanam dalam sistem grid terstruktur memungkinkan arah yang benar dipilih tanpa perlu menyimpan informasi tambahan. Untuk setiap elemen (i, j), permukaan dengan indeks lebih besar dari i atau j adalah positif sementara permukaan dengan indeks lebih kecil dari i atau j dikalikan dengan tanda negatif. Ini menjelaskan tanda negatif dalam Persamaan (6.11) dan (6.14).
6.3.3.1 Indeks Diskritisasi
Selain indeks lokal dan global, ada jenis lain yang dikenal sebagai indeks diskritisasi kadang-kadang digunakan, di mana lapangan-lapangan dan kuantitas geometris didefinisikan berdasarkan posisi atau nilai-nilai tetangga mereka. Mengacu pada Gambar 6.7c, gradien pada elemen (i, j) dapat dihitung menggunakan indeks diskritisasi sebagai berikut
Dengan demikian, algoritma untuk menghitung gradien dapat dituliskan sebagai berikut,

