17.9 Menghitung Jarak Normal ke Dinding
Menghitung jarak normal ke dinding. Pada model turbulensi BSL dan SST, jarak normal ke dinding terdekat diperlukan di seluruh domain untuk menentukan antarmuka antara wilayah komputasi k − ε dan k − ω, seperti yang tercermin oleh Persamaan (17.42) untuk model BSL dan (17.47) untuk model SST. Prosedur pencarian untuk menghitung
sangat mahal secara komputasi dalam situasi tiga dimensi bahkan untuk grid tetap. Situasinya menjadi lebih buruk dengan grid yang bergerak karena pencarian harus diulang pada setiap langkah waktu. Hal ini telah mendorong para pekerja untuk memperkenalkan perkiraan dalam perhitungan
yang mengakibatkan kesalahan besar.
Untuk menghindari prosedur pencarian yang mahal, teknik berdasarkan pemecahan persamaan diferensial untuk telah dikembangkan. Metode-metode ini didasarkan pada pemecahan persamaan Poisson, Eikonal, atau Hamilton-Jacobi [50–53]. Daya tarik dalam persamaan-persamaan ini adalah komposisinya yang melibatkan operator gradien dan/atau Laplacian yang tersedia dalam pemecah CFD. Hal ini membuat pendekatan ini mudah diimplementasikan, stabil, dan ekonomis terutama dengan grid yang bergerak.
Dengan mengadopsi pendekatan mirip Poisson, persamaan diferensial berikut untuk variabel φ diselesaikan:
tertunduk pada
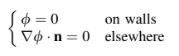
Jarak normal ke dinding terdekat dihitung menggunakan nilai yang diprediksi dari φ dan gradiennya sebagai
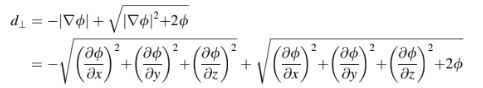
Saat memecahkan masalah aliran turbulen, Persamaan (17.119) di-diskritkan pada jaringan grid yang dihasilkan untuk memecahkan masalah menggunakan metode volume hingga dan mengikuti prosedur yang dijelaskan dalam Bab 8. Selama prosedur solusi, solusi yang konvergen untuk Persamaan (17.119) pertama-tama diperoleh, dari mana jarak normal ke dinding dihitung, sebelum memecahkan masalah aliran turbulen. Merujuk ke Gambar 17.3, dan mengingat bahwa istilah didefinisikan sebagai
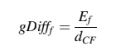
bentuk terdiskritisasi dari Persamaan (17.119) dapat ditulis sebagai
di mana
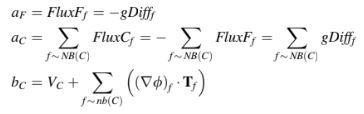

Gambar 17.3 Sebuah volume kontrol dua dimensi dengan besaran geometrisnya
Selain itu, kondisi batas Dirichlet dan Von Neumann yang dijelaskan oleh Persamaan (17.120) diperlakukan seperti yang dijelaskan di Bab 8. Setelah solusi untuk Persamaan (17.119), jarak normal ke dinding di semua pusat sel dalam domain dihitung menggunakan Persamaan (17.121) dengan gradien dihitung seperti yang dijelaskan di Bab 9.
