Merampingkan Koordinat
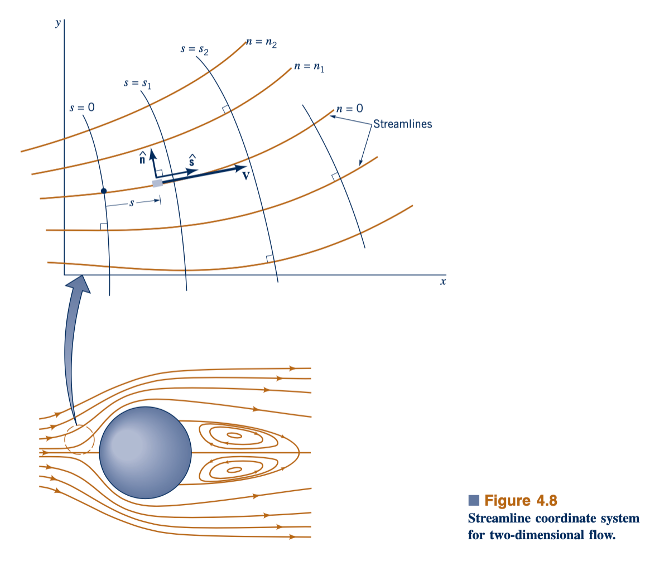
Dalam banyak situasi aliran, nyaman menggunakan sistem koordinat yang didefinisikan dalam hal garis arus aliran. Contohnya untuk aliran dua dimensi yang stabil diilustrasikan pada Gambar 4.8. Aliran seperti itu dapat dijelaskan baik dalam hal sistem koordinat kartesian x, y biasa (atau sistem lain seperti sistem koordinat polar r, u atau sistem koordinat garis arus). Dalam sistem koordinat garis arus, aliran dijelaskan dalam hal satu koordinat sepanjang garis arus, disebut s, dan koordinat kedua tegak lurus terhadap garis arus, disebut n. Vektor satuan dalam kedua arah ini dilambangkan dengan ˆs dan nˆ, seperti yang ditunjukkan dalam gambar. Perhatian diperlukan agar tidak membingungkan jarak koordinat s (skalar) dengan vektor satuan sepanjang arah garis arus, ˆs.
Bidang aliran oleh karena itu ditutupi oleh jaringan garis koordinat ortogonal melengkung. Pada setiap titik, arah s dan n saling tegak lurus, tetapi garis-garis dengan nilai s konstan atau n konstan tidak selalu lurus. Tanpa mengetahui lapangan kecepatan aktual (oleh karena itu, garis arus), tidak mungkin untuk membangun jaringan aliran ini. Dalam banyak situasi, asumsi vereinfachung yang tepat dapat dibuat sehingga kurangnya informasi ini tidak menjadi kesulitan yang tidak bisa diatasi. Salah satu keuntungan utama menggunakan sistem koordinat garis arus adalah bahwa kecepatan selalu sejajar dengan arah s. Artinya,
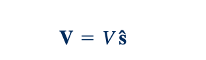
Hal ini memungkinkan penyederhanaan dalam menjelaskan percepatan partikel fluida dan dalam memecahkan persamaan yang mengatur aliran.
Untuk aliran stabil dua dimensi, kita dapat menentukan percepatan sebagai


dipilih sebagai garis koordinat, maka kecepatan selalu sejajar dengan arah aliran garis. Dengan demikian, dalam sistem koordinat garis aliran, komponen kecepatan dapat diekspresikan sebagai u = ds/dt dan v = 0. Dengan ini, komponen percepatan dapat ditentukan sebagai:
Ketika garis-garis tersebut melengkung, baik kecepatan partikel maupun arah alirannya dapat berubah dari satu titik ke titik lainnya. Secara umum, untuk aliran stabil baik kecepatan maupun arah alirannya adalah fungsi dari lokasi — V = V(s, n) dan ˆs =ˆs(s, n). Untuk suatu partikel yang diberikan, nilai s berubah seiring waktu, tetapi nilai n tetap karena partikel mengalir sepanjang garis aliran yang ditentukan oleh n = konstan. Oleh karena itu, penerapan aturan rantai memberikan:

Atau

Ini dapat disederhanakan dengan menggunakan fakta bahwa untuk aliran stabil tidak ada yang berubah seiring waktu di suatu titik tertentu sehingga baik 𝜕V/𝜕t maupun 𝜕ˆs/𝜕t adalah nol. Selain itu, kecepatan sepanjang garis aliran adalah V = ds/dt, dan partikel tetap berada di garis alirannya (n = konstan) sehingga dn/dt = 0. Oleh karena itu,

Kuantitas 𝜕ˆs/𝜕s mewakili batas saat 𝛿→ 0 dari perubahan vektor satuan sepanjang garis aliran, 𝛿ˆs, per perubahan jarak sepanjang garis aliran, 𝛿s. Magnitudo ˆs konstan (|𝑠| = 1; itu adalah vektor satuan), tetapi arahnya bervariasi jika garis alirannya melengkung. Dari Gambar 4.9 terlihat bahwa magnitudo dari 𝜕ˆs/𝜕s sama dengan invers dari radius lengkung dari garis aliran, r, pada titik yang dimaksud. Ini mengikuti karena kedua segitiga yang ditunjukkan (AOB dan A'O'B') adalah segitiga yang serupa sehingga 𝛿s/ℜ = |𝛿^𝑠 |/|𝛿𝑠| =|𝛿^𝑠|, 𝑎𝑡𝑎𝑢|𝛿^𝑠/𝛿𝑠|=1/ℜ. Demikian pula, dalam batas 𝛿s → 0, arah dari 𝛿ˆs/𝛿s terlihat tegak lurus terhadap garis aliran. Yaitu,

Oleh karena itu, percepatan untuk aliran dua dimensi yang stabil dapat ditulis dalam bentuk komponen sepanjang aliran dan normalnya seperti berikut:

Term pertama, a = V 𝜕V/𝜕s, mewakili percepatan konvektif sepanjang aliran, dan term kedua, an = V2/ℜ, mewakili percepatan sentrifugal (satu jenis percepatan konvektif) yang tegak lurus terhadap gerakan fluida. Komponen-komponen ini dapat diperhatikan pada Gambar E4.5 dengan meresolusi vektor percepatan menjadi komponen-komponennya sepanjang dan tegak lurus terhadap vektor kecepatan. Perhatikan bahwa vektor satuan nˆ diarahkan dari garis aliran ke pusat kelengkungan. Bentuk-bentuk percepatan ini digunakan dalam Bab 3 dan mungkin sudah familiar dari pertimbangan dinamika atau fisika sebelumnya.

