METODE GAUSS SEIDEL

Metode Gauss Seidel. Numerik volume hingga umumnya menggunakan metode iteratif untuk menyelesaikan setiap persamaan matriks. Metode ini menghitung solusi perkiraan untuk 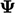$persamaan$ , yang menjadi lebih akurat dengan solusi berulang yang berurutan.

Metode berulanglebih disukai karena lebih efisien dibandingkan metode langsung, yang menyelesaikan persamaan matriks dengan tepat. Eliminasi Gaussian,yang merupakan dasar numerik untuk metode solusi langsung, memiliki biaya komputasi 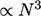$persamaan$ . Hal ini menjadi penghalang untuk banyak ukuran mesh dalam CFD volume terbatas.

Gauss-Seidel¹adalah metode sederhana dan berulang yang umumnya efektif untuk menyelesaikan persamaan transpor seperti contoh di Bagian. 5.1. Metode ini diilustrasikan dengan persamaan sampel

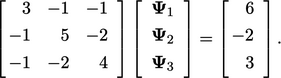2 3 2 3 2 3 3 1 1 1 6 66 1 5 2 77 66 2 77 = 66 2 77 : 4 5 4 5 4 5 1 2 4 3 3 \relax \special {t4ht=

(5.2)

Persamaan tersebut dapat ditulis ulang dengan: a) mengalikan koefisien off-diagonal dengan 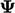$persamaan$ ; b) mengurangkan hasilnya dari ruas kanan (kanan); c) dan, membaginya dengan koefisien diagonal. yaitu :

$gambar\santai \khusus {t4ht=$

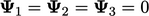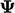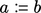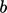Dimulai dengan, $persamaan$ , nilai baru $persamaan$ dihitung dengan Persamaan. (5.3a), Persamaan. (5.3b) dan Persamaan. (5.3c) secara berurutan, dimana notasi “ $persamaan$ ” menandakan “ $persamaan$ diberi nilai $persamaan$ ”.

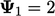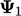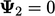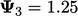Solusi pertama dari Persamaan. (5.3a) adalah $persamaan$ . Pembaruan $persamaan$ digantikan dalam Persamaan. (5.3b), yang solusinya adalah $persamaan$ . Kedua nilai yang diperbarui diganti dalam Persamaan. (5.3c) memberi $persamaan$ .

Proses ini kemudian diulangi dan melalui sapuan berturut-turut pada persamaan, solusinya menyatu seperti yang ditunjukkan di bawah ini.

Variabel	Awal	Sweep 1	…2	…3	…4

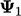$persamaan$	0,0000	2.0000	2.4167	2.7431	2.8821
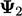$persamaan$	0,0000	0,0000	0,5833	0,8069	0,9121
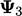$persamaan$	0,0000	1,2500	1.6458	1.8392	1.9266

Variabel	Sweep 5	…6	…7	…8	…9

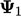$persamaan$	2.9462	2.9755	2.9888	2.9949	2.9977
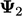$persamaan$	0,9599	0,9817	0,9916	0,9962	0,9983
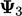$persamaan$	1.9665	1.9847	1.9930	1.9968	1,9985

Kesalahannya adalah 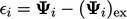$persamaan$ , yaitu perbedaan antara nilai perkiraan dan nilai eksak 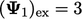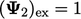$persam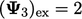aan$ , $persamaan$ dan $persamaan$ . Setelah 9 kali sapuan 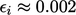$persamaan$ untuk semua variabel, yaitu dalam 0,2% dari solusi eksak.

Singkatnya, metode Gauss-Seidel adalah urutan perhitungan berikut 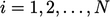$persamaan$ , diulangi hingga konvergensi:

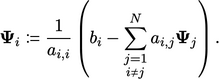0 1 N ℬ -1- BBb X a CC : i ai;i @ i j=1 i;j jA i⇔j \relax \special {t4ht=

(5.4)

Metode Gauss-Seidel, yang diterapkan pada matriks renggang , memiliki biaya komputasi 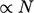$persamaan$ , sehingga praktis untuk simulasi dengan mesh besar yang sering terjadi pada CFD volume terbatas.

Konvergensi metode, dan langkah-langkah konvergensi untuk metode berulang secara umum, dibahas pada bagian berikut.