10.3 Metode Iteratif
Metode langsung umumnya tidak sesuai untuk menyelesaikan sistem persamaan besar, terutama ketika matriks koefisiennya bersparse, yaitu ketika sebagian besar elemen matriks adalah nol. Hal ini lebih jelas terjadi ketika sistem persamaan linear yang dilinearisasi bersifat non-linear dengan koefisien yang bergantung pada solusi, atau ketika menangani masalah yang bergantung pada waktu. Inilah jenis persamaan yang dihadapi ketika menyelesaikan masalah aliran fluida.
Sebaliknya, metode iteratif lebih menarik untuk masalah-masalah ini karena solusi dari sistem yang dilinearisasi menjadi bagian dari proses solusi iteratif. Ditambah lagi dengan kebutuhan penyimpanan komputer yang rendah dan biaya komputasi yang rendah dari pendekatan ini dibandingkan dengan metode langsung.
Terdapat banyak keluarga metode iteratif, dan untuk tinjauan menyeluruh terhadap pendekatan ini, pembaca disarankan untuk merujuk pada buku-buku khusus tentang topik ini [11–14]. Dalam bab ini, disajikan pemeriksaan singkat mengenai metode iteratif dasar bersama dengan penilaian terhadap algoritma multigrid yang umumnya digunakan untuk mengatasi kekurangan metode tersebut.
Metode langsung, seperti eliminasi Gauss dan dekomposisi LU, diperkenalkan semata-mata untuk menjelaskan beberapa proses numerik fundamental yang diperlukan untuk memahami metode iteratif.
Untuk menyatukan presentasi metode-metode ini, matriks koefisiennya akan ditulis dalam bentuk berikut:
dimana D, L, dan U merujuk pada matriks diagonal, matriks striktur bawah, dan matriks striktur atas, secara berturut-turut.
Metode iteratif untuk menyelesaikan sistem linear tipe menghitung serangkaian solusi
yang, jika beberapa kondisi terpenuhi, akan konvergen ke solusi yang tepat
Oleh karena itu, untuk solusi ini, dipilih suatu titik awal (yaitu,
dipilih sebagai kondisi awal atau tebakan awal) dan suatu prosedur iteratif yang menghitung
dari lapangan sebelumnya yang dihitung
dikembangkan. Sebuah iterasi “titik tetap” selalu dapat dikaitkan dengan sistem di atas dengan mendekomposisi matriks A sebagai
Dengan menggunakan dekomposisi ini, Persamaan (10.1) dapat dituliskan kembali sebagai
Menerapkan prosedur solusi iteratif titik tetap, Persamaan (10.48) menjadi
yang dapat dituliskan kembali dalam bentuk berikut:
di manadan
Pilihan berbeda untuk matriks-matriks ini menentukan metode iteratif yang berbeda.
Sebelum menjelaskan berbagai metode iteratif, akan disajikan sekumpulan karakteristik minimal yang harus dimiliki oleh suatu metode iteratif untuk menjamin konvergensi.
A. Persamaan iteratif dapat dituliskan saat konvergensi sebagai,
yang, setelah diubah urutan, menjadi
Dengan membandingkan Persamaan (10.52) dengan Persamaan (10.1), matriks koefisien diperoleh sebagai
atau, sebagai alternatif, sebagai
Hubungan ini antara berbagai matriks memastikan bahwa begitu solusi yang tepat dicapai, semua iterasi berikutnya tidak akan memodifikasinya.
B. Mulai dari suatu tebakan metode ini harus menjamin bahwa
akan konvergen ke
seiring dengan peningkatan n. Karena
dapat diungkapkan dalam hal
sebagai
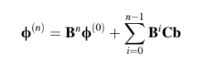
maka, untuk yang di atas menjadi benar, B harus memenuhi
Persamaan (10.56) menyiratkan bahwa radius spektral dari B harus kurang dari 1, yaitu
Kondisi ini menjamin bahwa metode iteratif bersifat self-corrective, yaitu, itu tangguh terhadap setiap kesalahan yang dimasukkan secara merugikan ke dalam vektor solusi Lebih banyak wawasan tentang kondisi di atas dapat diperoleh dengan mendefinisikan kesalahan
dalam solusi sebagai selisih antara nilai yang tepat dan nilai pada setiap iterasi (n), maka
Dengan mengurangkan Persamaan (10.51) dari Persamaan (10.50) dan menggunakan definisi dalam Persamaan (10.58), diperoleh hubungan antara kesalahan pada iterasi n dan n − 1 seperti
Dengan demikian, agar metode tersebut konvergen, hal berikut harus dipenuhi:
Untuk menerjemahkan Persamaan (10.60) menjadi sesuatu yang bermakna, diasumsikan bahwa vektor eigen dari B dianggap lengkap dan membentuk satu set penuh, yang berarti bahwa mereka membentuk dasar untukDalam hal ini, maka e dapat diungkapkan sebagai kombinasi linear dari N vektor eigen v dari B. Yaitu
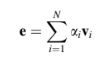
dengan setiap vektor eigen memenuhi
di manaadalah eigenvalue yang sesuai dengan vektor eigen
Dimulai dengan iterasi pertama, Persamaan (10.59) memberikan,
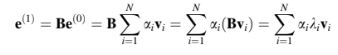
Untuk iterasi kedua, kesalahan diperoleh sebagai
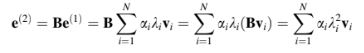
Prosedur ini dapat dilanjutkan dan dengan mudah dapat ditunjukkan melalui induksi bahwa
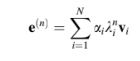
Oleh karena itu, agar prosedur iteratif konvergen saat n mendekati tak terhingga, semua eigenvalue harus kurang dari 1. Jika salah satunya lebih besar dari 1, maka kesalahan akan cenderung menuju tak terhingga. Ini menjelaskan pentingnya radius spektral ρ dari matriks B yang didefinisikan sebagai
yang telah disebutkan sebelumnya. Konvergensi metode iteratif dipercepat dengan mengurangi radius spektral matriks iteratif. Ini merupakan inti dari teknik iteratif.
C. Diperlukan suatu kriteria berhenti dalam metode iteratif. Banyak kriteria yang digunakan didasarkan pada variasi norma kesalahan residu yang didefinisikan sebagai
Salah satu kriteria adalah menemukan residu maksimum dalam domain dan menetapkan nilai residu tersebut menjadi kurang dari batas ambang ε untuk menyatakan bahwa solusi telah konvergen, yaitu
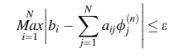
atau bahwa residu rata-rata akar kuadrat lebih kecil dari ε, yaitu
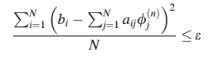
Kriteria lain yang mungkin adalah untuk perbedaan maksimum yang dinormalkan antara dua iterasi berturut-turut untuk turun di bawah ε. Kondisi ini dapat dituliskan sebagai
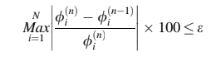
10.3.1 Metode Jacobi
10.3.2 Metode Gauss-Seidel
10.3.3 Prekondisioning dan Metode Iteratif
10.3.4 Teknik Dekomposisi Matriks
10.3.5 Dekomposisi LU yang Tidak Lengkap (ILU)
10.3.6 Faktorisasi LU yang Tidak Lengkap tanpa Pengisian ILU(0)
10.3.7 Algoritma Faktorisasi ILU(0)
10.3.8 Prekondisioner Faktorisasi ILU
10.3.9 Algoritma untuk Perhitungan D dalam Metode DILU
10.3.10 Algoritma Solusi Maju dan Mundur dengan Metode DILU
10.3.11 Metode Gradien untuk Menyelesaikan Sistem Aljabar
10.3.12 Metode Steepest Descent
10.3.13 Metode Gradien Konjugat
10.3.14 Metode Gradien Konjugat Bikonjugat (BiCG) dan BiCG Prekondisioning
