newtonian fuid

- Pada bagian 2.6 kita memperkenalkan gaya dalam fluida. Pada skala makroskopsis dari kontinum, kita mengarakterisasi respons fluida terhadap gaya yang diterapkan melalui model konstitutif.
- Fluida Newtonian atau fluida viskositas linear adalah model konstitutif yang paling umum yang mewakili perilaku banyak cairan dan gas. Model ini menyatakan bahwa sebuah fluida yang diam (atau bergerak dengan kecepatan konstan) tidak mempertahankan gaya geser
 ; hal ini dapat dinyatakan sebagai :
; hal ini dapat dinyatakan sebagai :
- Model tersebut merupakan representasi kontinum dari hukum viskositas Newton yang menyatakan bahwa gaya geser
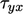 berkaitan secara proposional dengan gradien kecepatan oleh viskositas dinamis
berkaitan secara proposional dengan gradien kecepatan oleh viskositas dinamis 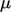 .
. - Ini adalah kasus khusus dari fluida stokesian yang lebih umum, didefinisikan sebagai
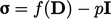 dimana D adalah laju deformasi pers. (2.33).
dimana D adalah laju deformasi pers. (2.33).
Modul Newtonian mengasumsikan :
- Fluida bersifat isotropis, artinya nilai
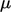 tidak bergantung pada arah dimana itu diukur;
tidak bergantung pada arah dimana itu diukur; - Viskositas bulk nol terkait dengan perubahan volume dari fluida.
- Menggunakan D dalam pers. (2.41) memastikan bahwa gaya geser hanya diinduki oleh deformasi. Mengambil bagian deviatorik, dev (D), memastikan bahwa tegangan viskos tidak dihasilkan oleh perubahan volume, yang direpresentasikan oleh
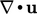 .
. - Ini disebabkan oleh operator “dev” yang mengurangi
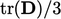 dari setiap komponen diagonal D, memberikan total tr(D) dari semua 3 komponen diagonal. Dari pers. (2.35),
dari setiap komponen diagonal D, memberikan total tr(D) dari semua 3 komponen diagonal. Dari pers. (2.35), 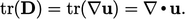
Pressure gradient
- Ketika kita substitusi pers. (2.41) dalam
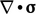 dalam pers. (2.19) tekanan menjadi
dalam pers. (2.19) tekanan menjadi 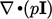 . Istilah
. Istilah 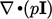 setara dengan gradien
setara dengan gradien 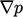 .
.
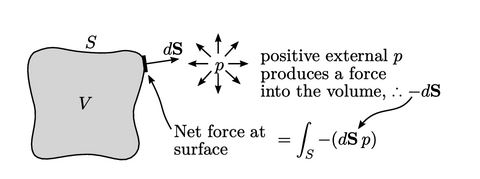
- Seperti divergensi dari tekanan pada pers. (2.22), gradien tekanan merepresentasikan aliran tekanan melintasi permukaan per satuan volume sebagai
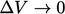 , sesuai dengan
, sesuai dengan
- Karena
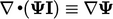 berlaku untuk variabel apapun eqn, sebuah term gradien bersifat konservatif, seperti divergensi, dan dapat dikonversi menjadi integral permukaan dalam teorema Gauss yang setara
berlaku untuk variabel apapun eqn, sebuah term gradien bersifat konservatif, seperti divergensi, dan dapat dikonversi menjadi integral permukaan dalam teorema Gauss yang setara
