NUMERICAL STABILITY
Kerancuan terkait kesalahan pemangkasan (urutan pertama untuk solusi fisik dan urutan kedua untuk yang tidak fisik) telah mendorong banyak peneliti untuk menyimpulkan bahwa karena perbedaan sentral dari istilah difusi sangat akurat, maka perbedaan sentral dari istilah konveksi juga seharusnya sama akuratnya. Tentu saja, seperti yang terlihat dalam bagian-bagian sebelumnya, perbedaan sentral dari istilah konveksi dapat menghasilkan solusi yang tidak fisik. Penyebab perilaku ini adalah bahwa skema perbedaan sentral tidak memiliki stabilitas konvektif bawaan ketika diterapkan pada turunan berorde ganjil seperti istilah konveksi. Leonard [9] mengemukakan konsep stabilitas konvektif sebagai penjelasan terhadap osilasi dalam solusi numerik yang dihasilkan dengan menerapkan skema perbedaan sentral pada aliran yang didominasi oleh konveksi. Leonard menggunakan persamaan konveksi-difusi satu dimensi umum dengan kecepatan konstan yang diberikan oleh
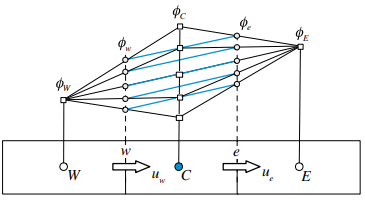
Gambar 11.9 Ketidakpekaan istilah konveksi CD terhadap nilai-nilai ϕC
untuk menggambarkan konsep ini. Ketika menerapkan persamaan ini di atas elemen centroid C yang ditunjukkan dalam Gambar 11.9, sisi kiri (LHS) mewakili laju perubahan ϕC dalam sel kontrol per unit waktu, dan sisi kanan (RHS) mewakili aliran neto melintasi permukaan elemen dan istilah sumber dalam elemen yang mempengaruhi nilai ϕC. Jika terdapat kesalahan numerik di RHS maka nilai ϕC yang dihitung dari Persamaan (11.73) akan meningkat atau berkurang tergantung pada skema yang digunakan dalam proses diskritisasi. Dalam skema yang tidak stabil, deviasi kecil dari nilai yang benar dari ϕC memberikan peningkatan/penurunan yang sesuai dalam aliran neto yang diwakili oleh RHS. Ketika prosedur iteratif digunakan sebagai bagian dari mekanisme solusi, peningkatan/penurunan dalam aliran neto akan lebih meningkatkan/menurunkan nilai ϕC pada setiap langkah berikutnya dari proses iteratif. Dalam skema yang stabil, perubahan dalam ϕC karena kesalahan di RHS harus memberikan umpan balik negatif ke RHS sebagai perangkat koreksi diri. Jelas, untuk stabilitas numerik seperti ini, RHS harus memenuhi
menunjukkan bahwa sensitivitas terhadap ϕC dari kombinasi istilah yang dimodelkan di sisi kanan Persamaan (11.73) seharusnya negatif. Dalam hal ini, peningkatan/penurunan ϕC akan sesuai dengan penurunan/kenaikan aliran masuk, yang pada gilirannya mendorong ϕC ke bawah/ke atas menuju nilai yang benar. Namun, stabilitas tidak boleh disamakan dengan terbatasnya atau akurasi. Skema numerik yang stabil sebenarnya bisa tidak terbatas sehingga menimbulkan overshoots/undershoots dan osilasi/getaran atau sangat difusif dan memberikan hasil yang rendah akurasinya. Stabilitas di sini mengacu pada pengendalian kesalahan numerik agar tetap terbatas agar tidak meningkat secara tak terbatas seperti yang terjadi pada skema perbedaan sentral di mana nilai terstandarisasi dari ϕC (Gambar 11.4) ditemukan bervariasi dari +∞ hingga −∞ sambil variasi Pe dari −∞ hingga +∞, meskipun nilai yang benar dari ϕC seharusnya bervariasi antara 1 dan 0. Kebetulan, skema upwind memiliki karakteristik terbatas dan stabil. Dengan ini diingat, bentuk diskritisasi umum dari RHS dari Persamaan (11.73) diberikan oleh

Jadi menggunakan skema perbedaan sentral, Persamaan (11.75) menjadi

Menganalisis skema perbedaan sentral menggunakan kriteria di atas, ditemukan bahwa untuk istilah difusi sensitivitasnya diberikan oleh
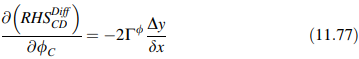
yang negatif karena Γ^ϕ positif, menunjukkan skema yang stabil. Namun, untuk suku konvektif persamaan sensitivitas memberikan
Yang sama dengan nol untuk aliran yang stabil namun tidak selalu untuk aliran tidak stabil. Untuk situasi yang tidak stabil, nilainya akan positif untuk aliran yang melambat. Pada aliran yang umum, wilayah-wilayah ini bertindak sebagai sumber goyangan dan dapat dengan mudah menyebabkan bencana numerik total ketika jumlah Péclet cukup besar. Bahkan untuk aliran yang stabil, karena nilainya nol, ia tidak dapat memberikan umpan balik ke dalam persamaan untuk bertindak sebagai perangkat koreksi diri. Persamaan (11.78) juga menunjukkan bahwa untuk aliran stabil, flux konvektif bersih yang dihitung dengan skema CD independen dari nilai ϕC. Oleh karena itu, seperti yang ditunjukkan pada Gambar 11.9, berbagai nilai yang mungkin dari ϕC akan menghasilkan flux konvektif bersih yang sama di atas elemen centroid C.
Dengan skema hulu angin, RHS dapat diperoleh dari Persamaan (11.36) sebagai

Sensitivitas diharapkan negatif karena skema tersebut ditemukan stabil untuk semua nomor Péclet, memang

yang mana negatif atau sama dengan nol untuk semua aliran. Ini akan sama dengan nol ketika kedua laju aliran massa negatif, sebuah situasi yang tidak muncul dalam situasi satu dimensi dari area penampang konstan. Ketika ditambahkan dengan difusi palsu yang diperkenalkan oleh pendekatan orde pertama, Persamaan (11.80) menunjukkan bahwa skema ini sangat stabil. Namun, stabilitas ini dicapai dengan mengorbankan akurasi, seperti yang telah ditunjukkan dalam bagian sebelumnya.
Untuk skema downwind, RHS diberikan oleh:

Sensitivitas diberikan oleh:

yang selalu positif atau sama dengan nol untuk semua aliran. Ketika ini ditambahkan dengan efek anti-difusi, itu memberikan skema yang sangat tidak stabil.
