OpenFOAM®
Teknik-teknik numerik yang diperkenalkan sejauh ini digunakan dalam apa yang berikutnya untuk mengembangkan aplikasi OpenFOAM® [27] untuk menyelesaikan persamaan Navier-Stokes tak berkompressibel.
15.10.2.1 Pada bagian ini, solvers Pressure Correction SIMPLE dibahas.
Berdasarkan algoritma SIMPLE, beberapa solver akan dikonstruksi. Solver dasar, simpleFoam, akan disajikan terlebih dahulu. Ini diikuti oleh sejumlah versi, di mana masing-masing menambahkan lebih banyak kemampuan ke dalam kode dasar. Solver ini dapat diringkas sebagai berikut:
1. simpleFoam (bukan solver bawaan OpenFOAM®) adalah kode dasar yang mencakup Algoritma SIMPLE dalam bentuk paling dasarnya.
2. simpleFoamImproved memperluas kode dasar untuk memungkinkan perawatan relaksasi yang ditingkatkan.
3. simpleFoamTransient menambahkan kemampuan transien ke dalam simpleFoam steady-state.
4. simpleFoamBuoyancy menambahkan ke dalam kode perlakuan gaya tubuh.
Lebih banyak versi akan dibahas di bab-bab berikutnya, masing-masing dengan kemampuan yang diperluas, ditambahkan dengan memodifikasi kode dasar yang dijelaskan dalam bab ini. Daftar versi yang akan dibahas dalam bab-bab berikutnya diberikan di bawah ini.
5. simpleFoamCompressible adalah versi yang dapat dikompresi dari simpleFoam (Bab 16).
6.simpleFoamTurbulent mencakup kemampuan untuk mengobati aliran turbulen (Bab 17).
simpleFoam
Sebelum meninjau kode simpleFoam, beberapa masalah notasi dasar dibahas. Langkah pertama adalah mendefinisikan, seperti yang ditunjukkan dalam Listing 15.2, lapangan dan parameter geometris yang akan diinisialisasi dan digunakan dalam kode.

In Listing 15.2, direktif makro #include di luar fungsi utama diperlukan untuk mendefinisikan jenis objek yang kemudian dideklarasikan dan digunakan dalam aplikasi. #include "fvCFD.H" berisi daftar definisi kelas-kelas yang umumnya diperlukan untuk membangun aplikasi apa pun di OpenFOAM®. Dalam aplikasi yang dikembangkan, sebuah header tambahan, yang tidak ada dalam header fvCFD.H, yang diperlukan untuk implementasi solver SIMPLE akan ditambahkan.
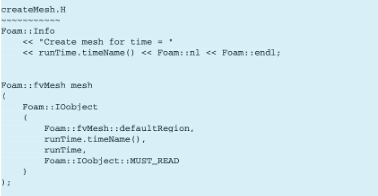
Penggunaan pernyataan #include di dalam fungsi utama adalah prosedur pengompakan, di mana setiap pernyataan yang dideklarasikan mewakili sebuah bagian dari kode yang dipindahkan ke nama file yang sesuai. Misalnya, pernyataan #include "createMesh.H" hanya mewakili kode yang ditunjukkan dalam Listing 15.3, yang diperlukan untuk menginisialisasi kelas mesh.
Setelah inisialisasi yang diperlukan dilakukan, langkah berikutnya adalah mendefinisikan lapangan atau variabel yang diperlukan oleh solver. Ini didefinisikan dalam file "createFields.H". Lapangan pertama yang didefinisikan, seperti yang ditunjukkan dalam Listing 15.4, adalah lapangan tekanan (p).

Karena solusinya diperoleh dengan menyelesaikan persamaan koreksi tekanan daripada persamaan tekanan, sebuah lapangan koreksi tekanan (pp) juga didefinisikan (Listing 15.5).

Perlu dicatat bahwa dalam Listing 15.5, sebuah konstruktor yang berbeda digunakan untuk mendefinisikan lapangan koreksi tekanan. Karena korektor tekanan mewakili tekanan itu sendiri, kondisi batas yang sama yang didefinisikan untuk tekanan sesungguhnya dapat digunakan untuk lapangan koreksi tekanan tanpa perlu mendefinisikan kuantitas yang sama dua kali.
Daftar jenis batas tekanan yang ditampilkan dalam Listing 15.6 sekarang disalin di bawah variabel pbt dalam Listing 15.5 dan langsung digunakan dalam konstruktor pp.

Korektor harus mengatur ulang lapangan koreksi menjadi nol pada setiap iterasi dan juga harus menerapkan nilai nol di semua batas di mana kondisi batas Dirichlet digunakan untuk tekanan.
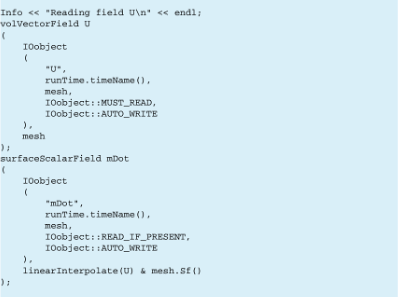
Lapangan kecepatan dan massa yang sesuai juga harus didefinisikan. Seperti yang digambarkan dalam Listing 15.7, lapangan kecepatan didefinisikan melalui file masukan sementara lapangan massa dapat didefinisikan sebagai jumlah terbitan.
Akhirnya, properti termo-fisik fluida juga harus didefinisikan. Untuk aliran laminar tak berkompressibel, ini melibatkan hanya memberikan nilai pada viskositas kinematik nu, seperti yang ditunjukkan dalam Listing 15.8.

Setelah mendefinisikan semua variabel, implementasi algoritma SIMPLE dapat dilanjutkan. Sebuah perulangan while dapat digunakan untuk kasus-kasus di mana kriteria berhenti adalah jumlah iterasi SIMPLE. Untuk setiap iterasi tunggal, persamaan momentum dan koreksi tekanan dipecahkan dan pembaruan variabel dilakukan. Memulai dengan persamaan momentum ditulis sebagai (bentuk yang dipecahkan dalam OpenFOAM®),
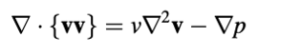
di mana viskositas kinematik ν didefinisikan sebagai
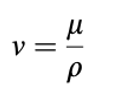
dan p mewakili tekanan dibagi oleh kepadatan, yaitu
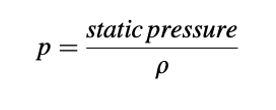
Solusinya diterjemahkan ke dalam skrip yang ditunjukkan dalam Listing 15.9.

Instruksi pertama dalam Listing 15.9 mendefinisikan diskritisasi volume terbatas dari persamaan momentum dalam bentuk vektor dengan matriks penyimpanannya (tiga komponen vektor kecepatan dipecahkan secara terpisah meskipun implementasinya vektor). Sistem kemudian direlaksasi secara implisit dan dipecahkan melalui solver iteratif.
Setelah persamaan momentum terselesaikan, diperoleh tebakan baru untuk lapangan kecepatan. Kecepatan ini pada umumnya tidak memenuhi persamaan kontinuitas dan perakitan persamaan kontinuitas dalam bentuk persamaan koreksi tekanan sekarang diperlukan untuk memperbaiki lapangan aliran. Persamaan koreksi tekanan ditulis sebagai
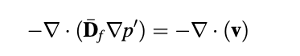
di mana komponen dari D pada pusat elemen dihitung sebagai
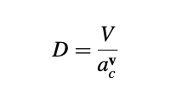
dengan nilai-nilai di wajah-wajah diperoleh dengan interpolasi. Implementasinya diterjemahkan ke dalam sintaks berikut (Listing 15.10):

di mana div(mDot) pada dasarnya adalah ∑𝑚𝑓, sementara pp mewakili p′ dan diatur ulang menjadi nol pada setiap iterasi. Selain itu, variabel DUf adalah nilai D di wajah sel yang diperoleh, seperti yang ditunjukkan dalam Listing 15.11, dengan interpolasi linear menggunakan nilai-nilai di simpul-simpul yang melintasi wajah. Selanjutnya, .A() mewakili istilah diagonal dalam matriks momentum dibagi oleh volume.

Listing 15.12 menghitung laju aliran massa di wajah sel (mDot) menggunakan interpolasi Rhie-Chow di mana perhitungan dari ∇pf dan ∇pf jelas ditunjukkan.

Persamaan koreksi tekanan sekarang sepenuhnya disetel dan dipecahkan dengan mengeksekusi pernyataan dalam Listing 15.13.
Setelah persamaan koreksi tekanan terselesaikan, lapangan kecepatan, tekanan, dan laju aliran massa diperbarui menggunakan lapangan koreksi tekanan yang diperoleh. Memulai dengan lapangan laju aliran massa (yaitu aliran mDot), ini diperbarui dengan mengeksekusi pernyataan di bawah ini (Listing 15.14).

Fungsi flux() dalam Listing 15.14 menyediakan perkalian matriks, koefisien matriks diagonal tambahan, dan solusi yang sesuai. Mengingat diskritisasi volume terbatas dari istilah difusi, setiap diagonal ekstra dari koefisien matriks mewakili sebuah wajah dari mesh. Dengan demikian, pembaruan dari aliran dapat dilakukan dengan cara yang lebih konsisten menggunakan langsung koefisien matriks dan nilai sel. Versi yang disederhanakan dari fungsi flux() ditunjukkan dalam Listing 15.15.
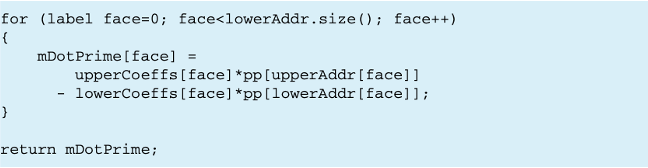
Dalam Listing 15.15, aliran koreksi mDotPrime (Persamaan 15.101) pada dasarnya dievaluasi dengan melakukan loop melalui wajah-wajah menggunakan koefisien atas dan bawah matriks dan mengalikan koefisien ini dengan nilai sel yang sesuai.
Terakhir, kecepatan dan tekanan di pusat sel diperbarui menggunakan skrip yang ditunjukkan dalam Listing 15.16.

di mana variabel URF adalah faktor relaksasi eksplisit untuk pembaruan tekanan λp, yang diperlukan untuk solver SIMPLE yang stabil.
simpleFoamImproved
Dalam simpleFoamImproved, interpolasi Rhie-Chow diperluas untuk memperhitungkan relaksasi lapangan kecepatan. Ini diterjemahkan ke dalam sintaks yang disajikan di bawah ini dalam Listing 15.17 yang memperluas interpolasi Rhie-Chow generik untuk memasukkan istilah tambahan dalam Persamaan (15.196).

Oleh karena itu, lapangan mdotf.prevIter() dan U.prevIter() perlu didefinisikan.
simpleFoamTransient
Dalam simpleFoamTransient, interpolasi Rhie-Chow diperluas untuk memperhitungkan istilah transien. Dengan demikian, ekspresi untuk laju aliran massa menjadi (Listing 15.18).

Selain itu, perulangan utama dimodifikasi untuk menambahkan perulangan transien, dengan kode utama menjadi seperti yang ditunjukkan dalam Listing 15.19.

simpleFoamBuoyancy
Solver simpleFoamBuoyancy menambahkan ke simpleFoamTransient kemampuan-kemampuan berikut: (i) penyelesaian persamaan energi, (ii) penambahan istilah sumber tubuh dalam persamaan momentum, dan (iii) perhitungan efek redistribusi istilah gaya tubuh dalam interpolasi Rhie-Chow.
Kode-kode yang digunakan untuk memperkenalkan modifikasi ini ditunjukkan dalam Listing (15.20), (15.21), dan (15.22).
Kode yang diperlukan untuk menyelesaikan persamaan energi diberikan dalam Listing (15.20).

Istilah sumber dalam persamaan momentum diimplementasikan seperti yang ditunjukkan dalam Listing (15.21)

sedangkan perhitungan aliran massa menggunakan interpolasi Rhie-Chow adalah seperti yang ditampilkan dalam Listing (15.22).

