2.4 Operasi Tensor dan Tensor
Operasi tensor dan tensor. Tensor dapat dianggap sebagai perluasan dari ide-ide yang sudah digunakan ketika mendefinisikan kuantitas seperti skalar dan vektor. Sebuah skalar adalah tensor berorde nol, dan sebuah vektor adalah tensor berorde satu. Tensor berorde yang lebih tinggi (2, 3, dll.) dapat dikembangkan, dan penggunaan utamanya adalah untuk memanipulasi dan mentransformasikan set persamaan. Karena dalam cakupan buku ini hanya diperlukan tensor berorde dua, mereka akan disebut hanya sebagai tensor.
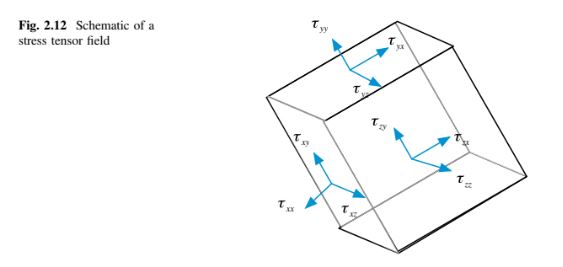
Mirip dengan vektor kecepatan aliran v, tensor tegangan deviatorik s (Gambar 2.12) akan sering disebutkan dalam buku ini dan digunakan di sini untuk mengilustrasikan operasi tensor. Jika x, y, dan z mewakili arah dalam sistem koordinat kartesian ortonomal, maka tensor tegangan s dan transpose-nya yang ditandai dengan superskrip direpresentasikan dalam bentuk komponennya sebagai,

Mirip dengan menuliskan vektor dalam hal komponennya, dengan mendefinisikan vektor satuan i, j, dan k dalam arah x, y, dan z secara berturut-turut, tensor s yang diberikan oleh Persamaan (2.65) dapat dituliskan dalam bentuk komponennya sebagai,
Persamaan (2.66) memungkinkan untuk mendefinisikan jenis produk vektor ketiga untuk mengalikan dua vektor, yang dikenal sebagai produk diadik, dan menghasilkan sebuah tensor dengan komponennya yang dibentuk oleh pasangan terurut dari kedua vektor tersebut. Secara khusus, produk diadik,
dari sebuah vektor v dengan dirinya sendiri, yang muncul dalam formulasi persamaan momentum aliran fluida, memberikan,

Gradien dari sebuah vektor v adalah sebuah tensor yang diberikan oleh,

Jumlah dua tensor dan
adalah sebuah tensor
yang komponennya adalah jumlah dari komponen yang sesuai dari kedua tensor tersebut, yaitu,
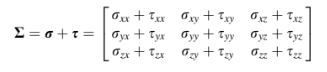
Mengalikan sebuah tensor s dengan sebuah skalar s menghasilkan sebuah tensor di mana komponennya dikalikan dengan skalar tersebut, yaitu,
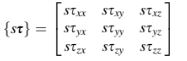
Hasil dari produk dot (dot product) antara tensor s dengan vektor v menghasilkan vektor berikut:

yang saat diperluas menjadi,

Menggunakan Persamaan (2.8), Persamaan (2.72) disederhanakan menjadi,
Persamaan di atas dapat diperoleh menggunakan perkalian matriks sebagai berikut,
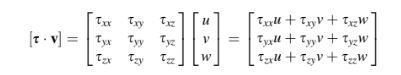
Secara mirip, divergensi dari sebuah tensor s ditemukan sebagai sebuah vektor yang diberikan oleh,
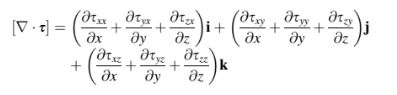
Produk titik ganda dari dua tensordan
adalah sebuah skalar yang dihitung sebagai,

Nilai akhir diperoleh dengan memperluas produk di atas dan melakukan produk titik ganda pada berbagai suku. Sebagai contoh,
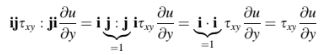
Dengan melakukan langkah-langkah yang sama pada setiap suku dalam produk yang diperluas, bentuk akhir dari diperoleh sebagai,
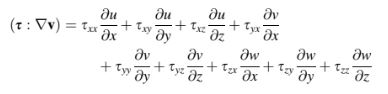
Baca juga: Teorema Dasar Kalkulus Vektor
