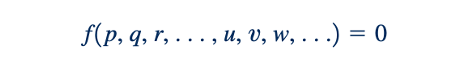Salah satu langkah paling penting dan sulit dalam menerapkan analisis dimensional pada suatu masalah adalah pemilihan variabel yang terlibat. Seperti yang disebutkan sebelumnya, untuk kenyamanan, kami akan menggunakan istilah variabel untuk menunjukkan setiap jumlah yang terlibat, termasuk konstanta dimensional dan nondimensional. Tidak ada prosedur sederhana di mana variabel dapat dengan mudah diidentifikasi. Umumnya, seseorang harus mengandalkan pemahaman yang baik tentang fenomena yang terlibat dan hukum fisika yang mengaturnya. Jika variabel yang tidak perlu disertakan, maka terlalu banyak pi term akan muncul dalam solusi akhir, dan mungkin sulit, memakan waktu, dan mahal untuk menghilangkan ini secara eksperimental. Jika variabel penting dihilangkan, maka hasil yang salah akan diperoleh; dan sekali lagi, hal ini mungkin sulit dan mahal untuk dipastikan. Oleh karena itu, sangat penting bahwa waktu dan perhatian yang cukup diberikan pada langkah pertama di mana variabel ditentukan.
Kebanyakan masalah rekayasa melibatkan asumsi penyederhanaan tertentu yang memengaruhi variabel yang harus dipertimbangkan. Biasanya kita ingin menjaga masalah sesederhana mungkin, bahkan jika beberapa akurasi dikorbankan. Keseimbangan yang sesuai antara kesederhanaan dan akurasi adalah tujuan yang diinginkan. Seberapa "akurat" solusi harus tergantung pada tujuan studi; yaitu, kita mungkin hanya peduli dengan tren umum dan, oleh karena itu, beberapa variabel yang diyakini hanya memiliki pengaruh minor dalam masalah dapat diabaikan untuk kesederhanaan.
Untuk sebagian besar masalah rekayasa (termasuk di luar mekanika fluida), variabel yang relevan dapat dikelompokkan ke dalam tiga kelompok umum—geometri, sifat material, dan efek eksternal.
Geometri. Karakteristik geometris biasanya dapat dijelaskan dengan serangkaian panjang dan sudut. Dalam sebagian besar masalah, geometri sistem memainkan peran penting, dan sejumlah variabel geometri yang mencukupi harus dimasukkan untuk menjelaskan sistem tersebut. Variabel-variabel ini biasanya dapat diidentifikasi dengan mudah.
Sifat Bahan. Karena respon suatu sistem terhadap efek eksternal yang diterapkan seperti gaya, tekanan, dan perubahan suhu tergantung pada sifat material yang terlibat dalam sistem, sifat-sifat material yang menghubungkan efek-efek eksternal dan respons harus dimasukkan sebagai variabel. Sebagai contoh, untuk fluida Newtonian, viskositas fluida adalah sifat yang menghubungkan gaya yang diterapkan dengan laju deformasi fluida. Ketika perilaku material menjadi lebih kompleks, seperti halnya pada fluida non-Newtonian, penentuan sifat-sifat material menjadi sulit, dan kelas variabel ini dapat sulit diidentifikasi.
Efek Eksternal. Istilah ini digunakan untuk menyebut setiap variabel yang menghasilkan, atau cenderung menghasilkan, perubahan dalam sistem. Sebagai contoh, dalam mekanika struktur, gaya (baik terkonsentrasi maupun terdistribusi) yang diterapkan pada suatu sistem cenderung mengubah geometrinya, dan gaya-gaya tersebut perlu dipertimbangkan sebagai variabel yang relevan. Untuk mekanika fluida, variabel dalam kelas ini akan terkait dengan tekanan, kecepatan, atau gravitasi.
Kelas variabel umum di atas dimaksudkan sebagai kategori yang luas yang seharusnya membantu dalam mengidentifikasi variabel-variabel. Namun, kemungkinan besar akan ada variabel penting yang tidak mudah dimasukkan ke dalam salah satu dari kategori di atas, dan setiap masalah perlu dianalisis secara hati-hati.
Karena kita ingin menjaga jumlah variabel tetap minimal, penting bahwa semua variabel bersifat independen. Sebagai contoh, jika dalam suatu masalah kita mengetahui bahwa momen inersia dari luas area piringan lingkaran adalah variabel penting, kita bisa mencantumkan baik momen inersia maupun diameter piringan sebagai variabel yang relevan. Namun, tidak perlu untuk menyertakan kedua momen inersia dan diameter, asalkan diameter masuk ke dalam masalah hanya melalui momen inersia. Secara lebih umum, jika kita memiliki masalah di mana variabel-variabel tersebut bersifat