Penerapan Persamaan Energi
Dalam Persamaan 5.64, istilah ∂/ ∂t (ρe) mewakili laju perubahan waktu dari energi total yang disimpan, e, dari isi volume kontrol. Istilah ini nol ketika aliran adalah stabil. Istilah ini juga nol dalam rata-rata ketika aliran adalah stabil dalam rata-rata (siklikal). Dalam Persamaan 5.64, integrannya
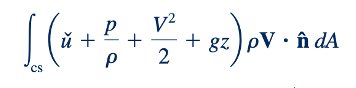
dapat menjadi tidak nol hanya di mana fluida melintasi permukaan kontrol (V⋅n≠0). Selain itu, V⋅n nol dan integrannya nol untuk bagian tersebut dari permukaan kontrol. Jika properti dalam tanda kurung, u, p/ρ V2/ V , dan gz, diasumsikan merata di seluruh area penampang aliran yang terlibat, integrasi menjadi sederhana dan memberikan

Selain itu, jika hanya ada satu aliran masuk dan keluar dari volume kontrol, maka

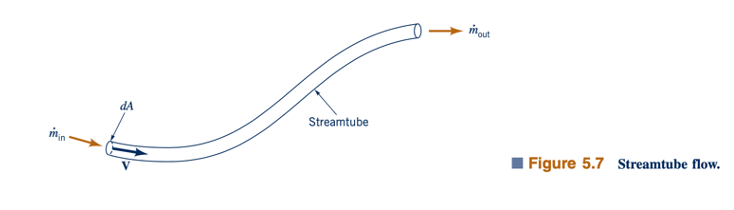
Aliran seragam seperti yang dijelaskan di atas akan terjadi dalam sebuah streamtube dengan diameter yang sangat kecil seperti yang diilustrasikan dalam Gambar 5.7. Jenis aliran streamtube ini mewakili aliran stabil dari sebuah partikel fluida sepanjang garis jalur. Kita juga dapat menyederhanakan kondisi aktual dengan mengabaikan ketidakhomogenan dalam penampang aliran yang terbatas. Kita menyebut ini sebagai aliran satu dimensi, dan meskipun aliran seragam seperti itu jarang terjadi dalam kenyataan, kesederhanaan yang dicapai dengan pendekatan satu dimensi seringkali membenarkan penggunaannya. Detail lebih lanjut tentang efek distribusi kecepatan nonuniform dan variabel aliran fluida lainnya dipertimbangkan dalam Bagian 5.3.4 dan dalam Bab 8, 9, dan 10.
Jika kerja poros terlibat, aliran harus tidak stabil, setidaknya secara lokal (lihat Ref. 1 dan 22). Aliran dalam setiap mesin fluida yang melibatkan kerja poros adalah tidak stabil di dalam mesin tersebut. Sebagai contoh, kecepatan dan tekanan di lokasi tetap dekat bilah berputar dari sebuah kipas adalah tidak stabil. Namun, di hulu dan hilir mesin, aliran mungkin stabil. Paling sering, kerja poros terkait dengan aliran yang tidak stabil secara berkala atau siklis. Dalam basis rata-rata waktu untuk aliran yang satu dimensi, siklis, dan melibatkan hanya satu aliran fluida masuk dan keluar
volume kontrol, seperti pengering rambut yang ditunjukkan dalam gambar di sisi margin, Persamaan 5.64 dapat disederhanakan dengan bantuan Persamaan 5.9 dan 5.66 untuk membentuk

Kami menyebut Persamaan 5.67 sebagai persamaan energi satu dimensi untuk aliran stabil dalam rata-rata. Perhatikan bahwa Persamaan 5.67 berlaku untuk aliran tak berkekambuhan dan berkekambuhan. Seringkali, sifat fluida yang disebut entalpi, ℎ, di mana

digunakan dalam Persamaan 5.67. Dengan entalpi, persamaan energi satu dimensi untuk aliran stabil dalam rata-rata menjadi:

Persamaan 5.69 sering digunakan untuk memecahkan masalah aliran yang dapat dipadatkan. Contoh 5.20 dan 5.21 mengilustrasikan bagaimana Persamaan 5.67 dan 5.69 dapat digunakan.


Jika aliran adalah stabil, satu dimensi, dan hanya melibatkan satu aliran fluida, maka kerja poros adalah nol dan persamaan energinya adalah:
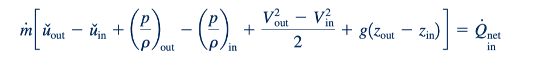
Kami menyebut Persamaan 5.70 sebagai persamaan energi aliran satu dimensi yang stabil. Persamaan ini berlaku untuk aliran tak berkekambuhan dan berkekambuhan. Untuk aliran berkekambuhan, entalpi paling sering digunakan dalam persamaan energi aliran satu dimensi yang stabil dan, oleh karena itu, kita memiliki:

Sebuah contoh penerapan Persamaan 5.70 akan menyusul.


