Penerapan Persamaan Momen-Momentum
Kita menyederhanakan penggunaan Persamaan 5.42 kita dalam beberapa cara:
1. Kami mengasumsikan bahwa aliran yang dipertimbangkan bersifat satu dimensi (distribusi seragam kecepatan rata-rata di setiap bagian).

2. Kami membatasi diri pada aliran yang mantap atau mantap dalam arti rata-rata siklus. Dengan demikian,

pada setiap saat untuk aliran mantap atau berdasarkan rata-rata waktu untuk aliran tidak mantap siklik.
3. Kami hanya bekerja dengan komponen dari Persamaan 5.42 yang terpecah sepanjang sumbu rotasi.
Pertimbangkan sprinkler yang berputar seperti yang digambarkan pada Gambar 5.4. Karena arah dan besarnya aliran melalui sprinkler dari inlet [bagian 112] ke outlet [bagian 122] lengan berubah, air memberikan torsi pada kepala sprinkler sehingga cenderung berputar atau benar-benar berputar sesuai dengan arah yang ditunjukkan, mirip dengan rotor turbin. Dalam menerapkan persamaan momen-momentum, kita memilih untuk menggunakan volume kontrol yang tetap dan tidak mengalami deformasi seperti yang ditunjukkan pada Gambar 5.4. Volume kontrol berbentuk cakram ini memuat dalam batasnya kepala sprinkler yang berputar atau diam dan bagian air yang mengalir melalui sprinkler yang terdapat di dalam volume kontrol pada suatu saat tertentu. Permukaan kontrol memotong material padat dari kepala sprinkler sehingga torsi poros yang menghambat gerakan dapat diidentifikasi dengan jelas. Ketika sprinkler berputar, medan aliran dalam volume kontrol diam bersifat siklus dan tidak stabil tetapi stabil secara rata-rata. Kita melanjutkan untuk menggunakan komponen aksial dari persamaan momen-momentum untuk menganalisis aliran ini.
Integran suku aliran momen-momentum pada Persamaan. 5.42,

Bisa tidak nol hanya di mana fluida menyeberangi permukaan kontrol. Di tempat lain pada permukaan kontrol, istilah ini akan nol karena V⋅n =0. Air memasuki volume kontrol secara aksial melalui batang holow sprinkler di bagian (1). Pada bagian permukaan kontrol ini, komponen dari r×V yang terselesaikan sepanjang sumbu rotasi adalah nol karena, seperti yang diilustrasikan oleh gambar di bagian margin, r×V terletak dalam bidang dari seksi (1), tegak lurus terhadap sumbu rotasi. Dengan demikian, tidak ada aliran momen-momentum aksial pada bagian (1). Air meninggalkan volume kontrol melalui masing-masing dari dua lubang nozzle di bagian (2). Untuk aliran keluar, magnitudo komponen aksial dari r×V adalah r2 Vu2 , di mana r2 adalah radius dari sumbu rotasi ke garis tengah nozzle dan V u2 adalah nilai komponen tangensial dari kecepatan aliran yang keluar dari setiap nozzle seperti yang diamati dari suatu bingkai referensi yang terpasang pada volume kontrol yang tetap dan tidak mengalami deformasi. Kecepatan fluida yang diukur relatif terhadap suatu permukaan kontrol tetap adalah kecepatan absolut, V.
Kecepatan absolut dan relatif, V dan W, terkait melalui hubungan vektor yang disebut sebagai

di mana U adalah kecepatan dari nozzle yang bergerak seperti yang diukur relatif terhadap permukaan kontrol tetap. Produk silang dan produk dot yang terlibat dalam istilah aliran momen-momentum dari Persamaan 5.42 adalah:

Setiap hasil dari produk silang dan produk dot dapat berupa nilai positif atau negatif. Untuk aliran ke dalam volume kontrol, V.n Setiap hasil dari produk silang dan produk dot dapat berupa nilai positif atau negatif. Untuk aliran ke dalam volume kontrol, V⋅n negatif. Untuk aliran keluar, V⋅n positif. Arah relatif dari r, V, dan r×V, serta tanda aljabar yang benar untuk menetapkan komponen sumbu dari r×V dapat ditentukan dengan menggunakan aturan tangan kanan. Arah positif sepanjang sumbu rotasi adalah arah di mana ibu jari tangan kanan menunjuk ketika itu diperpanjang, dan jari-jari yang tersisa ditekuk mengelilingi sumbu rotasi dalam arah positif rotasi seperti yang diilustrasikan dalam Gambar 5.5. Arah komponen aksial dari r×V secara serupa dapat ditentukan dengan mencatat arah hasil perkalian silang antara radius dari sumbu rotasi, r^ , dan komponen tangensial dari kecepatan absolut, Vu . Dengan demikian, untuk sprinkler pada Gambar 5.4, kita dapat menyatakan bahwa

di mana, karena konservasi massa, m adalah laju aliran massa total melalui kedua nozzle. Seperti yang ditunjukkan dalam Contoh 5.7, laju aliran massa tetap sama apakah sprinkler berputar atau tidak. Tanda aljabar yang benar dari komponen aksial dari r×V dapat dengan mudah diingat dengan cara berikut: jika V0 dan U berada dalam arah yang sama, gunakan + ; jika V0 dan U berada dalam arah yang berlawanan, gunakan − .
Selanjutnya, istilah torsi [∑(𝑟 𝑥 𝐹)𝑐𝑜𝑛𝑡𝑒𝑛𝑡𝑠 𝑜𝑓 𝑡ℎ𝑒 𝑐𝑜𝑛𝑡𝑟𝑜𝑙 𝑣𝑜𝑙𝑢𝑚𝑒] pada Persamaan 5.422 dianalisis. Memperhatikan torsi yang bertindak terhadap sumbu rotasi saja, kita menyimpulkan bahwa torsi poros penting. Torsi bersih terhadap sumbu rotasi yang terkait dengan gaya normal yang diberikan pada isi volume kontrol akan sangat kecil, jika tidak nol. Torsi aksial bersih akibat gaya tangensial fluida juga sangat kecil untuk volume kontrol pada Gambar 5.4. Dengan demikian, untuk sprinkler pada Gambar 5.4

Perhatikan bahwa kami telah memasukkan T poros sebagai jumlah positif dalam Persamaan 5.45. Ini setara dengan mengasumsikan bahwa T berada dalam arah yang sama dengan rotasi.
Untuk sprinkler pada Gambar 5.4, komponen aksial dari persamaan momen-momentum adalah, dari Persamaan 5.44 dan 5.45:

Kami menafsirkan Tporos sebagai jumlah negatif dari Persamaan 5.46 untuk berarti bahwa torsi poros sebenarnya menentang rotasi lengan sprinkler seperti yang ditunjukkan pada Gambar 5.4. Torsi poros, T poros , menentang rotasi pada semua perangkat turbin.

Kita bisa mengevaluasi daya poros, W poros , yang terkait dengan torsi poros, T poros , dengan membentuk persamaan antara torsi poros dan kecepatan rotasi poros, ω. [Kita menggunakan notasi bahwa perkalian dari T poros dan W = pekerjaan ( .),= d ( )/dt , dan dengan demikian W = daya]. Dengan demikian, dari Persamaan 5.46 kita mendapatkan:
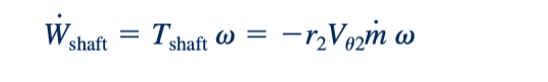
Dikarenakan r2 w adalah kecepatan dari setiap nozzle sprinkler, U, kita juga dapat menyatakan Persamaan 5.47 dalam bentuk
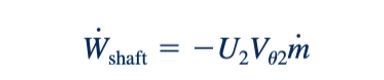
Kerja poros per satuan massa, w poros yang kita peroleh, sama dengan W poros/m . Dengan membagi Persamaan 5.48 dengan laju aliran massa, m,
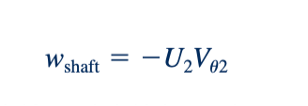
Kerja poros negatif seperti dalam Persamaan 5.47, 5.48, dan 5.49 adalah kerja keluar dari volume kontrol, yaitu kerja yang dilakukan oleh fluida pada rotor dan oleh porosnya.
Prinsip-prinsip yang terkait dengan contoh sprinkler ini dapat diperluas untuk menangani sebagian besar aliran turbin yang disederhanakan. Teknik dasarnya tidak sulit. Namun, geometri dari beberapa aliran turbin cukup rumit.
Contoh 5.18 juga menggambarkan bagaimana komponen aksial dari persamaan momen-momentum (Eq. 5.46) dapat digunakan.


Ketika persamaan momen-momentum (Eq. 5.42) diterapkan pada aliran yang lebih umum, satu dimensi melalui mesin yang berputar, kita memperoleh:
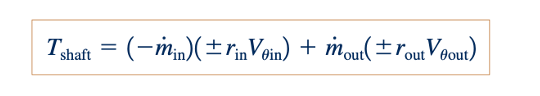
dengan menerapkan jenis analisis yang sama yang digunakan dengan sprinkler pada Gambar 5.4. "-" digunakan dengan laju aliran massa masuk ke volume kontrol, m,in , dan "+" digunakan dengan laju aliran massa keluar dari volume kontrol, m˙out , untuk memperhitungkan tanda dari hasil kali dot, V⋅n, yang terlibat. Apakah "+" atau "-" digunakan dengan produk r×V tergantung pada arah dari rV𝜃. Cara sederhana untuk menentukan tanda dari produk rV𝜃 adalah dengan membandingkan arah dari V𝜃 dan kecepatan baling-baling, U. Seperti yang ditunjukkan pada bagian margin, jika V𝜃 dan U berada dalam arah yang sama, maka produk rV𝜃 adalah positif. Jika V𝜃 dan U berada dalam arah yang berlawanan, maka produk rV0 adalah negatif. Tanda dari torsi poros adalah "+" jika T poros berada dalam arah yang sama sepanjang sumbu rotasi dengan w, dan "-" jika tidak.
Daya poros, W poros , terkait dengan torsi poros, T poros, dengan persamaan:

Dengan menggunakan Persamaan 5.50 dan 5.51 dengan tanda "" untuk T poros dalam Persamaan 5.50, kita memperoleh:

atau karena rw=U

"+" digunakan untuk produk UV𝜃 ketika U dan V𝜃 berada dalam arah yang sama; "-" digunakan ketika U dan V𝜃 berada dalam arah yang berlawanan. Juga, karena + Tporos digunakan untuk mendapatkan Persamaan 5.53, W poros. Ketika W poros positif, daya masuk ke dalam fluida (misalnya, pada pompa), dan ketika W poros negatif, daya keluar dari fluida (misalnya, pada turbin).
Kerja poros per satuan massa, w poros , dapat diperoleh dari daya poros, W poros , dengan membagi Persamaan 5.53 dengan laju aliran massa, m. Dengan konservasi massa,

Dari Persamaan 5.53, kita mendapatkan:

Penerapan Persamaan 5.50, 5.53, dan 5.54 ditunjukkan dalam Contoh 5.19. Lebih banyak contoh penerapan Persamaan 5.50, 5.53, dan 5.54 disertakan dalam Bab 12.


