Penerapan Persamaan Momentum Linier
Persamaan momentum linear untuk volume kontrol inersial adalah persamaan vektor Eq. 5.22. Dalam aplikasi rekayasa, komponen persamaan vektor ini yang diurai sepanjang koordinat ortogonal, misalnya, x, y, dan z (sistem koordinat kartesian) atau r, θ, dan z (sistem koordinat silinder), biasanya akan digunakan. Sebagai contoh sederhana yang melibatkan aliran stabil dan tak dapat dikompres, akan dipertimbangkan terlebih dahulu.





Beberapa generalitas penting tentang penerapan persamaan momentum linear (Eq. 5.22) tampak dalam contoh yang baru saja dipertimbangkan:
1. Ketika aliran terdistribusi secara merata di atas suatu bagian permukaan kontrol tempat aliran masuk atau keluar dari volume kontrol terjadi, operasi integral disederhanakan. Oleh karena itu, aliran satu dimensi lebih mudah untuk dikerjakan daripada aliran yang melibatkan distribusi kecepatan nonuniform.
2. Momentum linear memiliki arah; dapat memiliki komponen dalam hingga tiga arah koordinat ortogonal. Selain itu, di sepanjang setiap koordinat, momentum linear dari sebuah partikel fluida bisa ke arah positif atau negatif, dan oleh karena itu dianggap sebagai kuantitas positif atau negatif. Dalam Contoh 5.11, hanya momentum linear dalam arah z yang dipertimbangkan (semuanya berada dalam arah negatif z dan oleh karena itu dianggap sebagai negatif).
3. Aliran momentum linear positif atau negatif ke dalam volume kontrol melibatkan produk V⋅n^ negatif. Aliran momentum keluar dari volume kontrol melibatkan produk V⋅n^ positif. Tanda aljabar yang benar (− atau +) yang diberikan kepada aliran momentum (VrV⋅n^ dA) akan bergantung pada arah kecepatan (positif dalam arah koordinat positif, negatif dalam arah koordinat negatif) dan produk V⋅n^ (untuk aliran keluar dari volume kontrol, untuk aliran masuk ke volume kontrol). Ini ditunjukkan dalam gambar di pinggir halaman. Dalam Contoh 5.11, aliran momentum ke dalam volume kontrol melalui bagian (1) adalah kuantitas positif, sementara aliran momentum keluar dari volume kontrol melalui bagian (2) adalah kuantitas negatif.
4. Laju perubahan momentum linear dari isi volume kontrol yang tidak terdeformasi (yaitu,𝜕/𝜕t ∫ CV ρVdV) adalah nol untuk aliran yang. Masalah momentum yang dipertimbangkan dalam teks ini semuanya melibatkan aliran yang stabil.
5. Jika permukaan kontrol dipilih sehingga tegak lurus terhadap aliran di mana fluida masuk atau keluar dari volume kontrol, gaya permukaan yang diberikan di lokasi ini oleh fluida di luar volume kontrol pada fluida di dalam akan disebabkan oleh tekanan. Selanjutnya, ketika aliran subsonik keluar dari volume kontrol ke atmosfer, tekanan atmosfer berlaku di bagian penyeberangan keluar. Dalam Contoh 5.11, aliran tersebut bersifat subsonik dan oleh karena itu kami menetapkan tekanan aliran keluar pada level atmosfer. Persamaan kontinuitas (Eq. 5.12) memungkinkan kami mengevaluasi kecepatan aliran fluida w dan w di bagian (1) dan (2).
6. Gaya yang disebabkan oleh tekanan atmosfer yang bertindak pada permukaan kontrol mungkin perlu dipertimbangkan seperti yang ditunjukkan oleh Persamaan 13 dalam Contoh 5.11 untuk gaya reaksi antara nozzle dan fluida. Ketika menghitung gaya jangkar, F, gaya-gaya akibat tekanan atmosfer pada permukaan kontrol saling membatalkan satu sama lain (misalnya, setelah menggabungkan Persamaan 12 dan 13, gaya-gaya tekanan atmosfer tidak lagi terlibat) dan tekanan gage dapat digunakan.
7. Gaya-gaya eksternal memiliki tanda aljabar—positif jika gaya tersebut berada dalam arah koordinat positif yang ditetapkan dan negatif jika sebaliknya.
8. Hanya gaya-gaya eksternal yang bertindak pada isi volume kontrol yang dipertimbangkan dalam persamaan momentum linear (Eq. 5.22). Jika hanya fluida yang termasuk dalam volume kontrol, gaya-gaya reaksi antara fluida dan permukaan atau permukaan yang kontak dengan fluida (permukaan basah) akan perlu dimasukkan dalam Eq. 5.22. Jika fluida dan permukaan yang terbasahi berada dalam volume kontrol, gaya-gaya reaksi antara fluida dan permukaan yang terbasahi tidak muncul dalam persamaan momentum linear (Eq. 5.22) karena mereka merupakan gaya internal, bukan gaya eksternal. Namun, gaya jangkar yang menahan permukaan yang terbasahi adalah gaya eksternal, dan oleh karena itu harus dimasukkan dalam Eq. 5.22.
9. Gaya yang diperlukan untuk mengikat suatu benda umumnya akan ada sebagai respons terhadap gaya tekanan permukaan dan/atau gaya geser yang bertindak pada permukaan kontrol, terhadap perubahan aliran momentum linear melalui volume kontrol yang berisi benda, dan terhadap berat benda dan fluida yang terkandung dalam volume kontrol. Dalam Contoh 5.11, gaya pengikat nozzle diperlukan terutama karena gaya tekanan dan sebagian karena perubahan aliran momentum linear yang terkait dengan percepatan fluida di nozzle. Berat air dan nozzle yang terkandung dalam volume kontrol hanya sedikit memengaruhi besarnya gaya jangkar.
Untuk lebih memperlihatkan penggunaan persamaan momentum linear (Eq. 5.22), kita pertimbangkan contoh aliran satu dimensi lainnya sebelum melanjutkan ke aspek-aspek lain dari persamaan penting ini.



Pada Contoh 5.10 dan 5.12, gaya yang diberikan pada fluida yang mengalir mengakibatkan perubahan arah aliran saja. Gaya ini terkait dengan pembatasan aliran, dengan sirip pada Contoh 5.10, dan dengan tikungan pipa pada Contoh 5.12. Pada Contoh 5.11, gaya yang diberikan pada fluida yang mengalir mengakibatkan perubahan hanya pada magnitudo kecepatan. Gaya ini terkait dengan sebuah nozzle yang menyempit. Gaya penambat diperlukan untuk menahan sebuah sirip atau saluran tetap. Mereka paling mudah diestimasi dengan volume kontrol yang mengandung sirip atau saluran dan fluida yang mengalir terlibat. Atau, dua volume kontrol terpisah dapat digunakan, satu berisi hanya sirip atau saluran dan yang lain berisi hanya fluida yang mengalir.








Semua contoh momentum linear yang dipertimbangkan sejauh ini melibatkan volume kontrol yang diam dan tidak berubah bentuk yang dengan demikian bersifat inersial karena tidak ada percepatan. Sebuah volume kontrol yang tidak berubah bentuk dan translasi dalam garis lurus dengan kecepatan konstan juga bersifat inersial karena tidak ada percepatan. Untuk sebuah sistem dan sebuah volume kontrol yang inersial, bergerak, tidak berubah bentuk yang keduanya bersamaan pada suatu saat tertentu, teorema transportasi Reynolds (Eq. 4.232) adalah:

di mana W adalah kecepatan relatif. Ketika kita menggabungkan Persamaan 5.23 dengan Persamaan 5.19 dan 5.20, kita mendapatkan:

Ketika persamaan yang menghubungkan kecepatan absolut, relatif, dan kontrol volume (Persamaan 5.14) digunakan dengan Persamaan 5.24, hasilnya adalah:
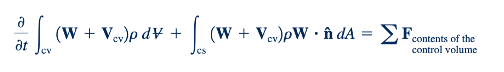
Untuk kecepatan kontrol volume yang konstan, Vcv , dan aliran yang stabil dalam kerangka acuan volume kontrol,

Juga, untuk volume kontrol inersial yang tidak berubah bentuk,

Untuk aliran yang mantap (baik pada basis seketika maupun rata-rata waktu), Persamaan 5.15 memberikan

Gabungan Persamaan 5.25, 5.26, 5.27, dan 5.28, kami menyimpulkan bahwa Persamaan momentum linear untuk volume kontrol inersial, bergerak, tidak terdeformasi yang melibatkan aliran mantap (seketika atau rata-rata waktu) adalah
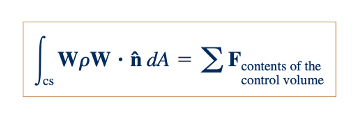
Contoh 5.17 mengilustrasikan penggunaan Persamaan 5.29.


