Pengaruh Variasi Luas Penampang Aliran
Ketika fluida mengalir secara mantap melalui suatu saluran yang memiliki luas penampang aliran yang bervariasi dengan jarak aksial, persamaan konservasi massa (kontinuitas)
Dalam aliran tak berkompressibilitas, kepadatan fluida tetap konstan dan kecepatan aliran dari bagian ke bagian bervariasi secara terbalik dengan luas penampang melintang. Namun, ketika aliran bersifat kompresibel, kepadatan, luas penampang melintang, dan kecepatan aliran dapat bervariasi dari bagian ke bagian. Kami melanjutkan untuk menentukan bagaimana kepadatan fluida dan kecepatan aliran berubah dengan lokasi aksial dalam saluran area variabel ketika fluida adalah gas ideal dan aliran melalui saluran adalah mantap dan isotropik.
Di Bab 3, hukum kedua Newton diterapkan pada aliran fluida yang tidak kental (bebas gesekan) dan mantap. Untuk arah sepanjang aliran, hasilnya (persamaan 3.52 baik untuk aliran yang dapat dikompresi maupun tidak dapat dikompresi)
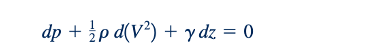
Aliran bebas gesekan dari bagian ke bagian melalui volume kontrol terbatas juga diatur oleh Persamaan 11.41, jika aliran tersebut satu dimensi, karena setiap partikel fluida yang terlibat akan memiliki pengalaman yang sama. Untuk aliran gas ideal, suku potensial perbedaan energi, 𝛾 dz, dapat diabaikan karena ukurannya yang kecil dibandingkan dengan suku lainnya, yaitu, dp dan d(V2). Dengan demikian, persamaan gerak yang tepat dalam arah sepanjang aliran untuk aliran mantap, satu dimensi, dan isotropik (adiabatik dan bebas gesekan) dari gas ideal diperoleh dari Persamaan 11.41 sebagai

Jika kita membentuk logaritma dari kedua sisi persamaan kontinuitas (Persamaan 11.40), hasilnya adalah:
Mendiferensialkan Persamaan 11.43, kita dapatkan:

Atau

Sekarang kita gabungkan Persamaan 11.42 dan 11.44 untuk mendapatkan:
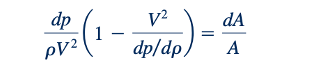
Karena aliran yang dipertimbangkan adalah isentropik, kecepatan bunyi terkait dengan variasi tekanan terhadap densitas oleh Persamaan 11.34, yang diulang di sini untuk kemudahan:

Persamaan 11.34, yang dikombinasikan dengan definisi dari bilangan Mach, menyatakan:
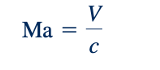
dan Persamaan 11.45 memberikan:

Persamaan 11.42 dan 11.47 digabungkan untuk membentuk:
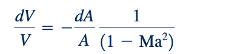
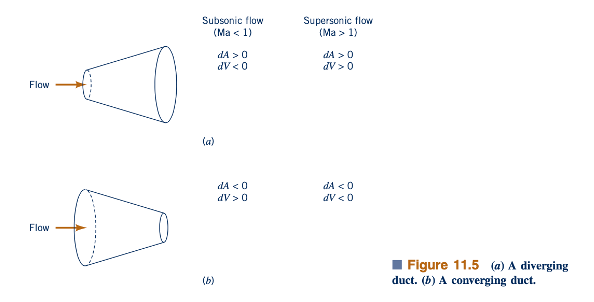
Kita dapat menggunakan Persamaan 11.48 untuk menyimpulkan bahwa ketika aliran bersubsonik (Ma ≤ 1), perubahan kecepatan dan area penampang berlawanan arah. Dengan kata lain, peningkatan area yang terkait dengan aliran bersubsonik melalui saluran melebar seperti yang ditunjukkan pada Gambar 11.5a disertai dengan penurunan kecepatan. Aliran bersubsonik melalui saluran menyusut seperti yang ditunjukkan pada Gambar 11.5b melibatkan peningkatan kecepatan. Kecenderungan ini konsisten dengan perilaku aliran yang tidak dapat dimampatkan, yang sudah kita bahas sebelumnya dalam buku ini, misalnya, di Bab 3 dan 8.
Persamaan 11.48 juga berguna untuk menunjukkan bahwa ketika aliran bersupersonik (Ma ≥ 1), perubahan kecepatan dan area bergerak ke arah yang sama. Saluran yang melebar (Gambar 11.5a) akan mempercepat aliran supersinik. Saluran yang menyempit (Gambar 11.5b) akan memperlambat aliran supersinik. Kecenderungan ini berlawanan dengan apa yang terjadi pada aliran yang tidak dapat dimampatkan dan aliran bersubsonik yang dapat dimampatkan.
Untuk lebih memahami mengapa aliran saluran bersubsonik dan bersupersonik begitu berbeda, kita menggabungkan Persamaan 11.44 dan 11.48 menjadi

Dengan menggunakan Persamaan 11.49, kita dapat menyimpulkan bahwa untuk aliran subsionik (Ma < 1), perubahan kepadatan dan luas berada dalam arah yang sama, sedangkan untuk aliran supersionik (Ma > 1), perubahan kepadatan dan luas berada dalam arah yang berlawanan. Karena ρAV harus tetap konstan (Persamaan 11.40), ketika saluran melebar dan aliran bersubsonik, baik kepadatan maupun luasnya meningkat dan dengan demikian kecepatan aliran harus menurun. Namun, untuk aliran supersionik melalui saluran yang melebar, ketika luasnya meningkat, kepadatannya turun sehingga kecepatan aliran harus meningkat untuk menjaga ρAV tetap konstan.
Dengan menyusun ulang Persamaan 11.48, kita dapat memperoleh

Persamaan 11.50 memberikan wawasan tentang apa yang terjadi ketika Ma = 1. Untuk Ma = 1, Persamaan 11.50 mengharuskan bahwa dA/dV =0. Hasil ini menunjukkan bahwa luas yang terkait dengan Ma = 1 adalah jumlah minimum atau maksimum.
Sebuah saluran yang menyempit-melebar (Gambar 11.6a dan foto di margin) melibatkan jumlah minimum area. Jika aliran yang memasuki saluran semacam itu bersifat subsionik, Persamaan 11.48 mengungkapkan bahwa kecepatan fluida akan meningkat di bagian menyempit dari saluran, dan pencapaian kondisi sonic (Ma = 1) di lokasi area minimum tampaknya mungkin. Jika aliran yang memasuki saluran menyempit-melebar adalah supersonik, Persamaan 11.48 menyatakan bahwa kecepatan fluida akan berkurang di bagian menyempit dari saluran dan kondisi sonic di area minimum adalah mungkin.