Pengukuran Debit Aliran
Banyak jenis perangkat yang menggunakan prinsip-prinsip yang terlibat dalam persamaan Bernoulli telah dikembangkan untuk mengukur kecepatan dan laju aliran fluida. Tabung Pitot-statis yang dibahas dalam Bagian 3.5 adalah contohnya. Contoh lain yang dibahas di bawah ini termasuk perangkat untuk mengukur laju aliran dalam pipa dan
Kanal dan perangkat untuk mengukur laju aliran dalam saluran terbuka. Dalam bab ini, kita akan mempertimbangkan alat pengukur aliran "ideal" - yang bebas dari efek viskos, kompresibilitas, dan efek "dunia nyata" lainnya. Koreksi untuk efek-efek ini dibahas dalam Bab 8 dan 10. Tujuan kita di sini adalah memahami prinsip dasar pengoperasian flowmeter sederhana ini.
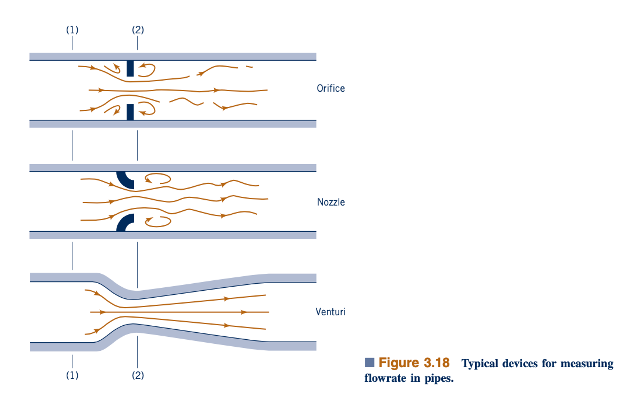
Salah satu cara yang efektif untuk mengukur laju aliran melalui pipa adalah dengan menempatkan jenis pembatasan di dalam pipa seperti yang ditunjukkan dalam Gambar 3.18 dan mengukur perbedaan tekanan antara bagian hulu dengan kecepatan rendah dan tekanan tinggi di bagian hulu (1) dan bagian hilir dengan kecepatan tinggi dan tekanan rendah di bagian hulu (2). Tiga jenis flowmeter yang umum digunakan diilustrasikan: meter orifice, meter nozzle, dan meter Venturi. Operasi masing-masing didasarkan pada prinsip fisik yang sama - peningkatan kecepatan menyebabkan penurunan tekanan. Perbedaan di antara mereka adalah masalah biaya, akurasi, dan seberapa dekat operasi sebenarnya mereka mematuhi asumsi aliran yang diidealisis.
Kita mengasumsikan aliran horizontal (z1=z2), mantap, tidak viscous, dan tidak dapat dipadatkan antara titik (1) dan (2). Persamaan Bernoulli menjadi
Efek aliran non-horizontal dapat dengan mudah dimasukkan dengan memasukkan perubahan elevasi, z1 - z2, dalam persamaan Bernoulli.
Jika kita mengasumsikan profil kecepatan seragam di bagian 112 dan 122, persamaan kontinuitas dapat ditulis sebagai
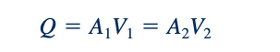
di mana A adalah area aliran kecil (A1 < A2) di bagian (2). Kombinasi dari kedua persamaan ini menghasilkan laju aliran teoritis sebagai berikut:
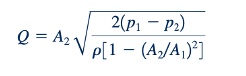
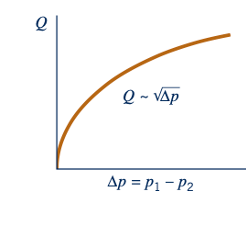
Oleh karena itu, seperti yang ditunjukkan oleh gambar di pinggir teks, untuk geometri aliran tertentu (A1 dan A2), laju aliran dapat ditentukan jika perbedaan tekanan, p1 - p2, diukur. Laju aliran yang sebenarnya, Q, akan lebih kecil dari hasil teoritis ini karena berbagai perbedaan antara "dunia nyata" dan asumsi yang digunakan dalam derivasi Persamaan 3.20. Perbedaan ini (yang cukup konsisten dan dapat sekecil 1 hingga 2% atau sebesar 40%, tergantung pada geometri yang digunakan) dapat diakomodasi dengan menggunakan koefisien debit yang diperoleh secara empiris seperti yang dibahas dalam Bagian 8.6.1.

Alat pengukur laju aliran lainnya berdasarkan persamaan Bernoulli digunakan untuk mengukur laju aliran dalam saluran terbuka seperti saluran air dan parit irigasi. Dua dari perangkat ini, pintu air dan weir berujung tajam, dibahas di bawah ini dengan asumsi aliran stabil, inviscid, tidak dapat dipadatkan. Perangkat-perangkat aliran terbuka ini dan yang lainnya dibahas secara lebih detail di Bab 10.
Pintu air seperti yang ditunjukkan pada Gambar 3.19a sering digunakan untuk mengatur dan mengukur laju aliran dalam saluran terbuka. Seperti yang ditunjukkan dalam Gambar 3.19b, laju aliran, Q, merupakan fungsi dari kedalaman air di hulu, z1, lebar pintu, b, dan pembukaan pintu, a. Penerapan persamaan Bernoulli dan persamaan kontinuitas antara titik (1) dan (2) dapat memberikan perkiraan yang baik terhadap laju aliran yang sebenarnya diperoleh. Kami mengasumsikan profil kecepatan seragam cukup jauh di hulu dan di hilir pintu.
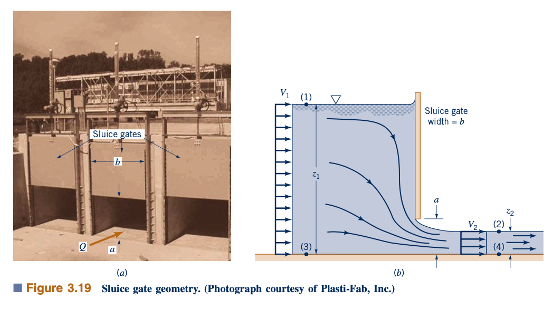
Dengan demikian, kita menerapkan persamaan Bernoulli antara titik pada permukaan bebas pada (1) dan (2) untuk memberikan.
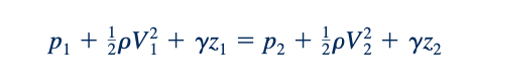
Juga, jika gerbang memiliki lebar yang sama dengan saluran sehingga A1= bz1 dan A2 = bz2, persamaan kontinuitas memberikan.
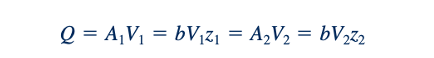
Dengan fakta bahwa p1= p2= 0, persamaan-persamaan ini dapat digabungkan dan diatur ulang untuk memberikan laju aliran sebagai
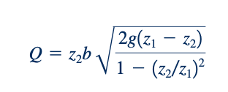
Pada batas z1 > z2, hasil ini secara sederhana menjadi
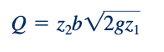
Hasil pembatas ini mewakili fakta bahwa jika rasio kedalaman, z1/z2, besar, energi kinetik fluida di hulu pintu gerbang diabaikan dan kecepatan fluida setelah jatuh sejauh (z1-z2) = z1 kira-kira V2= √2𝑔𝑧
Hasil dari Persamaan 3.21 juga dapat diperoleh dengan menggunakan persamaan Bernoulli antara titik 132 dan 142 serta fakta bahwa p3 ≈ 𝛾z1 dan p4 ≈ 𝛾z2 karena garis aliran di bagian-bagian ini lurus. Dalam formulasi ini, daripada energi potensial di (1) dan (2), kita memiliki kontribusi tekanan di (3) dan (4). Kedalaman di hulu, z2 , bukan pembukaan pintu gerbang, a, digunakan untuk mendapatkan hasil dari Persamaan 3.21.
Seperti yang dibahas terkait dengan aliran dari orifice (Gambar 3.142), fluida tidak dapat berbelok pada sudut 90° yang tajam. Sebuah vena contracta terbentuk dengan koefisien kontraksi, Cc= a/z2 , kurang dari 1. Biasanya,Cc sekitar 0.61 dalam rentang rasio kedalaman 0 < a/z1 < 0.2. Untuk nilai a/z1 yang lebih besar, nilai Cc meningkat dengan cepat.

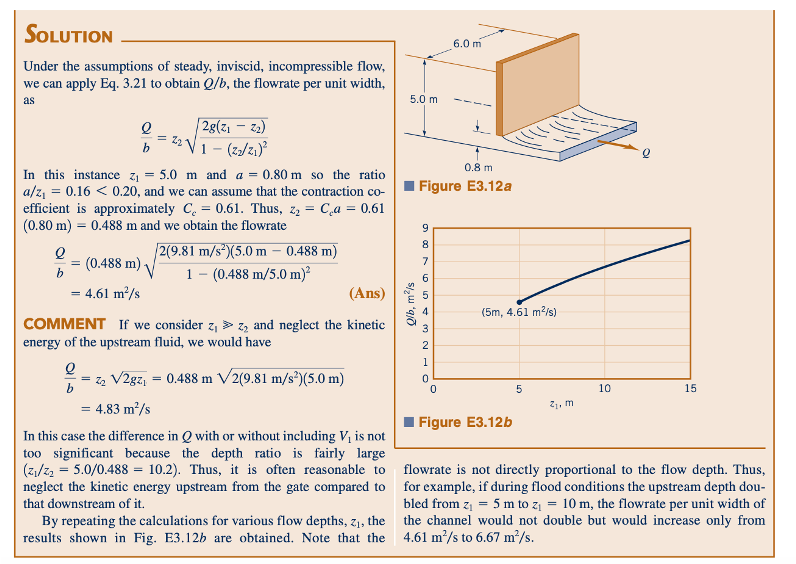
Salah satu alat yang digunakan untuk mengukur aliran dalam saluran terbuka adalah weir. Weir berbentuk persegi panjang dengan tepi tajam yang khas ditunjukkan dalam Gambar 3.20. Untuk perangkat seperti itu, laju aliran cairan di atas pelat weir tergantung pada tinggi weir, Pw, lebar saluran, b, dan tinggi air, H, di atas puncak weir. Penerapan persamaan Bernoulli dapat memberikan perkiraan sederhana dari laju aliran yang diharapkan untuk situasi-situasi ini, meskipun aliran sebenarnya cukup kompleks.
Antara titik (1) dan (2), medan tekanan dan gravitasi menyebabkan fluida berakselerasi dari kecepatan V1 menjadi kecepatan V2. Pada titik (1), tekanan adalah p1 = 𝛾h, sedangkan pada titik (2) tekanan pada dasarnya atmosferik, p2 = 0. Di sepanjang garis aliran melengkung tepat di atas permukaan atas pelat weir, bagian a–a2, tekanan berubah dari atmosferik di permukaan atas ke nilai maksimum tertentu dalam aliran fluida dan kemudian kembali ke atmosferik di permukaan bawah. Distribusi ini ditunjukkan dalam Gambar 3.20. Distribusi tekanan seperti itu, yang digabungkan dengan kelengkungan garis aliran dan gravitasi, menghasilkan profil kecepatan yang cukup tidak seragam di seluruh bagian ini. Distribusi kecepatan ini dapat diperoleh dari percobaan atau teori yang lebih canggih.
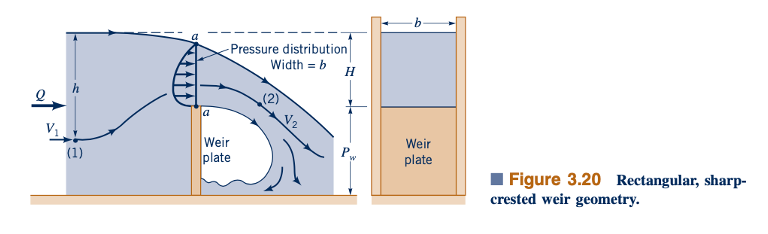
Untuk saat ini, kita akan mengambil pendekatan yang sangat sederhana dan mengasumsikan bahwa aliran weir mirip dalam banyak hal dengan aliran tipe orifice dengan garis aliran bebas. Dalam hal ini, kita dapat mengharapkan kecepatan rata-rata di sepanjang puncak weir akan sebanding dengan 1/2gH dan luas aliran untuk weir persegi panjang ini akan sebanding dengan Hb. Oleh karena itu, dapat disimpulkan bahwa
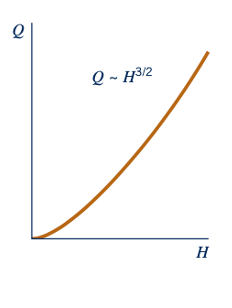
dimana C1 adalah sebuah konstanta yang akan ditentukan.
Penggunaan sederhana dari persamaan Bernoulli telah memberikan metode untuk menganalisis aliran yang relatif kompleks di atas weir. Dependensi fungsional yang benar dari Q terhadap H telah diperoleh Q∝H 3/2 (seperti yang ditunjukkan oleh gambar di pinggir), tetapi nilai koefisien C1 tidak diketahui. Bahkan analisis yang lebih canggih pun tidak dapat memprediksi nilainya secara akurat. Seperti yang dibahas di Bab 10, eksperimen digunakan untuk menentukan nilai C1.

