Penurunan Persamaan Energi
Hukum pertama termodinamika untuk sebuah sistem, dalam kata-kata,

Secara simbolik, pernyataan ini adalah

Atau

Beberapa variabel ini perlu penjelasan singkat sebelum melanjutkan lebih jauh. Energi total yang disimpan per satuan massa untuk setiap partikel dalam sistem, e, terkait dengan energi internal per satuan massa, u, energi kinetik per satuan massa, V2/2 , dan energi potensial per satuan massa, gz, oleh persamaan

Laju bersih perpindahan panas ke dalam sistem ditandai dengan Qnet in, dan laju bersih kerja yang masuk ke dalam sistem ditandai dengan Wnet in. Transfer panas dan transfer kerja dianggap "+" masuk ke dalam sistem dan "-" keluar.
Persamaan 5.55 berlaku untuk sistem referensi inersial dan non-inersial. Kita lanjutkan untuk mengembangkan pernyataan volume kontrol dari hukum pertama termodinamika. Untuk volume kontrol yang bertepatan dengan sistem pada suatu saat

Selain itu, untuk sistem dan isi dari volume kontrol yang bertepatan yang tetap dan tidak deformasi, teorema transportasi Reynolds (Persamaan 4.19) dengan parameter b disetel sama dengan e2 memungkinkan kita menyimpulkan bahwa

atau dengan kata-kata,

Dengan menggabungkan Persamaan 5.55, 5.57, dan 5.58, kita mendapatkan formula volume kontrol untuk hukum pertama termodinamika:

Energi total yang disimpan per satuan massa, e, dalam Persamaan 5.59 adalah untuk partikel-fluida yang masuk, keluar, dan berada di dalam volume kontrol. Penjelasan lebih lanjut tentang transfer panas dan transfer kerja yang terlibat dalam persamaan ini akan dijelaskan.
Laju transfer panas, Q , mewakili semua cara di mana energi ditukar antara isi volume kontrol dan sekitarnya karena adanya perbedaan suhu. Oleh karena itu, radiasi, konduksi, dan/atau konveksi mungkin terjadi. Seperti yang ditunjukkan oleh gambar di sisi margin, transfer panas ke dalam volume kontrol dianggap positif; transfer panas keluar dianggap negatif. Dalam banyak aplikasi rekayasa, prosesnya adalah adiabatik; laju transfer panas, Q˙ , adalah nol. Laju transfer panas bersih, Q˙net in , juga bisa nol ketika ∑𝑄 𝑖𝑛 −∑𝑄 𝑜𝑢𝑡 =0.
Laju transfer kerja, ˙W , yang juga disebut sebagai daya, adalah positif ketika kerja dilakukan pada isi v
volume kontrol oleh sekitarnya. Sebaliknya, dianggap negatif jika tidak. Kerja dapat ditransfer melintasi permukaan kontrol dalam beberapa cara. Dalam paragraf berikut, kita akan mempertimbangkan beberapa bentuk penting dari transfer kerja.
Dalam banyak kasus, kerja ditransfer melintasi permukaan kontrol oleh sebuah poros yang bergerak. Pada perangkat berputar seperti turbin, kipas, dan propelor, sebuah poros berputar mentransfer kerja melintasi bagian permukaan kontrol yang memotong poros tersebut. Bahkan pada mesin reciprocating seperti mesin pembakaran dalam internal dan kompresor yang menggunakan pengaturan piston-di-silinder, sebuah poros engkol berputar digunakan. Karena kerja adalah hasil kali antara gaya dan perpindahan terkait, laju kerja (atau daya) adalah hasil kali antara gaya dan perpindahan terkait per unit waktu. Untuk sebuah poros berputar, transfer daya, W shaft , terkait dengan torsi poros yang menyebabkan rotasi, T shaft , dan kecepatan sudut poros, ω, oleh hubungan:

Ketika permukaan kontrol memotong material poros, torsi poros dihasilkan oleh material poros di permukaan kontrol. Untuk memungkinkan pertimbangan masalah yang melibatkan lebih dari satu poros, kita menggunakan notasi
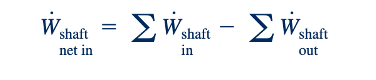

Transfer kerja juga dapat terjadi di permukaan kontrol ketika gaya yang terkait dengan tekanan normal fluida bertindak dalam jarak. Pertimbangkan aliran pipa sederhana yang diilustrasikan dalam Gambar 5.6 dan volume kontrol yang ditunjukkan. Untuk situasi ini, tegangan normal fluida, 𝜎, sama dengan negatif dari tekanan fluida, p, dalam semua arah; yaitu,

Hubungan ini dapat digunakan dengan jumlah perkiraan yang bervariasi untuk banyak masalah teknik (lihat Bab 6)
Perpindahan daya W, yang berhubungan dengan gaya F yang bekerja dengan benda yang bergerak dengan kecepatan V diberikan oleh perkalian titk F . V. Hal ini diilustrasikan oleh gambar dipinggir. oleh karena itu, transfer daya yang berhubungan dengan tegangan normal yang bekerja pada satu partikel fluida, & 𝛿W tegangan normal, dapat dievaluasi sebagai perkalian titik dari gaya tegangan normal, 𝛿F tegangan normal dan kecepatan partikel fluida , V , sebagai

Jika gaya tegangan normal diungkapkan sebagai hasil dari perkalian antara tegangan normal lokal, 𝜎 = - p, dan luas permukaan partikel fluida, n⋅𝛿A, maka hasilnya adalah:

Untuk semua partikel fluida pada permukaan kontrol dari Gambar 5.6 pada saat yang dipertimbangkan, transfer daya karena tegangan normal fluida, W normal stress , adalah

Perhatikan bahwa nilai W normal stress untuk partikel pada permukaan dalam basah pipa adalah nol karena V⋅n nol di sana. Dengan demikian, W normal stress hanya dapat tidak nol di tempat di mana fluida masuk dan keluar dari volume kontrol. Meskipun hanya aliran pipa sederhana yang dipertimbangkan, Persamaan 5.62 sangat umum, dan volume kontrol yang digunakan dalam contoh ini dapat berfungsi sebagai model umum untuk kasus lainnya.
Transfer kerja juga dapat terjadi di permukaan kontrol karena gaya-gaya tegangan tangensial. Kerja yang ditransfer oleh poros yang berputar disebabkan oleh gaya-gaya tegangan tangensial dalam bahan poros. Untuk sebuah partikel fluida, daya gaya-gaya geser, 𝛿W tangential stress , dapat dievaluasi sebagai hasil kali titik dari gaya-gaya tegangan tangensial, 𝛿F tangential stress, dan kecepatan partikel fluida, V. Artinya,
Untuk volume kontrol dari Gambar 5.6, kecepatan partikel fluida adalah nol di mana-mana pada permukaan dalam basah pipa. Dengan demikian, tidak ada kerja gaya-gaya tegangan tangensial yang ditransfer melintasi bagian permukaan kontrol tersebut. Selain itu, jika kita memilih permukaan kontrol sehingga tegangan gaya-gaya tegangan tangensial tegak lurus terhadap kecepatan partikel fluida, maka gaya-gaya tegangan tangensial juga tegak lurus terhadap kecepatan. Oleh karena itu, transfer kerja gaya-gaya tegangan tangensial adalah nol pada bagian permukaan kontrol tersebut. Ini diilustrasikan dalam gambar di sisi margin. Dengan demikian, secara umum, kita memilih volume kontrol seperti pada Gambar 5.6 dan menganggap transfer daya gaya-gaya tegangan tangensial fluida sangat kecil.
Dengan menggunakan informasi yang telah kita kembangkan tentang daya, kita dapat menyatakan hukum pertama termodinamika untuk isi volume kontrol dengan menggabungkan Persamaan 5.59, 5.60, dan 5.62 untuk memperoleh

Ketika persamaan untuk energi total yang disimpan (Persamaan 5.62) dipertimbangkan dengan Persamaan 5.63, kita mendapatkan persamaan energi:

