Penurunan Persamaan Kontinuitas
Prinsip kekekalan massa untuk sebuah sistem dinyatakan secara sederhana sebagai

Atau

di mana massa sistem, Msys, secara lebih umum diekspresikan sebagai

dan integrasi dilakukan di atas volume sistem. Dalam kata-kata, Persamaan 5.2 menyatakan bahwa massa sistem sama dengan jumlah semua produk elemen densitas-volume untuk isi sistem.
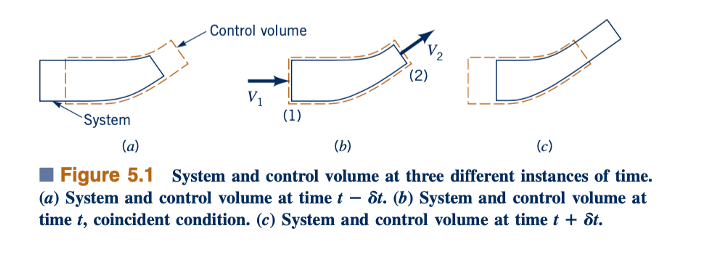
Untuk sebuah sistem dan sebuah volume kendali tetap yang tidak berdeformasi yang bertepatan pada suatu saat tertentu, seperti yang diilustrasikan dalam Gambar 5.1, teorema transportasi Reynolds (Persamaan 4.19) dengan B = massa dan b = 1 memungkinkan kita menyatakan bahwa

Atau

Dalam Persamaan 5.3, kita menyatakan laju perubahan waktu massa sistem sebagai jumlah dari dua kuantitas volume kendali, laju perubahan waktu massa isi volume kendali,

dan laju bersih aliran massa melalui permukaan kendali,

Ketika aliran adalah steady, semua sifat medan (yaitu, sifat-sifat di setiap titik yang ditentukan) termasuk kepadatan tetap konstan terhadap waktu dan laju perubahan waktu dari massa isi volume kendali adalah nol. Dengan kata lain,

Integrannya, V⋅ n^ dA, dalam integral laju aliran massa mewakili hasil kali komponen kecepatan, V, tegak lurus terhadap bagian kecil permukaan kendali dan luas permukaan diferensial, dA. Dengan demikian, V⋅ n^ dA adalah laju aliran volume melalui dA dan pV⋅ n^ dA adalah laju aliran massa melalui dA. Selanjutnya, seperti yang ditunjukkan dalam sketsa di pinggiran halaman, tanda hasil kali titik V⋅ n^ adalah "-" untuk aliran keluar dari volume kendali dan "+" untuk aliran masuk ke dalam volume kendali karena n^ dianggap positif ketika menunjuk keluar dari volume kendali. Ketika semua besaran diferensial, pV⋅n^ dA, dijumlahkan di seluruh permukaan kendali, seperti yang ditunjukkan oleh integral

hasilnya adalah laju aliran massa bersih melalui permukaan kendali, atau

di mana ˙m˙ adalah laju aliran massa (lbm/s, slug/s, atau kg/s). Jika integral dalam Persamaan 5.4 positif, maka aliran bersih keluar dari volume kontrol; jika integral negatif, aliran bersih masuk ke volume kontrol.
Persamaan volume kontrol untuk pelestarian massa, yang umumnya disebut persamaan kontinuitas, untuk volume kontrol yang tetap dan tidak mengalami deformasi diperoleh dengan menggabungkan Persamaan 5.1, 5.2, dan 5.3 menjadi:

Dalam kata-kata, Persamaan 5.5 menyatakan bahwa untuk melestarikan massa, laju perubahan massa dari isi volume kontrol ditambah dengan laju aliran massa bersih melalui permukaan kontrol harus sama dengan nol. Sebenarnya, hasil yang sama bisa diperoleh secara lebih langsung dengan menyamakan laju aliran massa masuk dan keluar dari volume kontrol dengan laju akumulasi dan pengurangan massa dalam volume kontrol (lihat Bagian 3.6.22). Namun, memperhatikan bahwa teorema transport Reynolds berlaku untuk kasus yang mudah dimengerti ini memberikan keyakinan tambahan. Keyakinan ini akan sangat membantu saat kita mengembangkan ekspresi volume kontrol untuk prinsip-prinsip penting lainnya.
Sebuah ungkapan yang sering digunakan untuk laju aliran massa, m, melalui sebuah bagian permukaan kontrol yang memiliki luas A adalah:

di mana ρ adalah kepadatan fluida, Q adalah laju aliran volume (ft3/s atau m3 /s), dan V adalah komponen kecepatan fluida yang tegak lurus terhadap luas A. Karena

Untuk menerapkan Persamaan 5.6, kita menggunakan nilai rata-rata atau representatif dari kepadatan fluida, p, dan kecepatan fluida, V. Pada aliran inkompresibel, p didistribusikan secara merata di atas luas penampang A. Pada aliran kompresibel, biasanya kita menganggap kepadatan fluida didistribusikan secara merata di setiap bagian aliran dan memperbolehkan perubahan kepadatan terjadi hanya dari bagian ke bagian lainnya. Kecepatan fluida yang sesuai untuk digunakan dalam Persamaan 5.6 adalah nilai rata-rata dari komponen kecepatan tegak lurus terhadap luas penampang yang terlibat. Nilai rata-rata ini, V, didefinisikan sebagai

Jika kecepatan, V, dianggap didistribusikan secara merata (aliran satu dimensi) di atas luas penampang, A, maka

