Penurunan Persamaan Momen-Momentum
Dalam banyak masalah rekayasa, momen dari sebuah gaya terhadap sebuah sumbu, yaitu, torsi, penting. Hukum kedua gerakan Newton telah membawa pada hubungan yang berguna antara gaya dan aliran momentum linear. Persamaan momentum linear juga dapat digunakan untuk memecahkan masalah yang melibatkan torsi. Namun, dengan membentuk momen dari momentum linear dan momen dari gaya resultant yang terkait dengan setiap partikel fluida dengan memperhatikan sebuah titik dalam sistem koordinat inersia, kita akan mengembangkan persamaan momen momentum yang menghubungkan torsi dan aliran momentum sudut untuk isi dari suatu volume kontrol. Ketika torsi penting, persamaan momen momentum sering lebih nyaman untuk digunakan daripada persamaan momentum linear.
Penerapan hukum kedua gerakan Newton pada sebuah partikel fluida menghasilkan
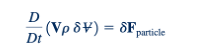
dimana V adalah kecepatan partikel yang diukur dalam sistem referensi inersia, p adalah kepadatan partikel, 𝛿∀ adalah volume partikel yang sangat kecil, dan 𝛿F partikel adalah resultan gaya luar yang bekerja pada partikel. Jika kita membentuk momen setiap sisi Persamaan. 5.30 sehubungan dengan titik asal sistem koordinat inersia, kita peroleh

dimana r adalah vektor posisi dari titik asal sistem koordinat inersial ke partikel fluida 1. Kami catat bahwa
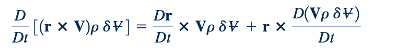
dan

Jadi, sejak itu
Dengan menggabungkan Persamaan 5.31, 5.32, 5.33, dan 5.34, kita dapatkan ekspresi


Persamaan 5.35 berlaku untuk setiap partikel dalam sebuah sistem. Untuk sebuah sistem, yaitu kumpulan partikel-fluida, kita perlu menjumlahkan kedua sisi dari Persamaan 5.35 untuk mendapatkan

dimana

Kami mencatat bahwa,

Karena urutan berurutan diferensiasi dan integrasi dapat dibalik tanpa konsekuensi. Ingatlah bahwa turunan material, D( )/Dt, menunjukkan turunan waktu mengikuti sistem tertentu; lihat Bagian 4.2.1.2. Dengan demikian, dari Persamaan 5.36 dan 5.38 kita mendapatkan

Atau

Sketsa di pinggiran menjelaskan apa itu torsi, T = r x F. Untuk suatu volume kontrol yang secara instan bersamaan dengan sistem, torsi yang bekerja pada sistem dan isi volume kontrol akan identik:


Selanjutnya, untuk sistem dan isi volume kontrol yang bersamaan dan tidak berubah bentuk, teorema transportasi Reynolds (Eq. 4.192) mengarah ke
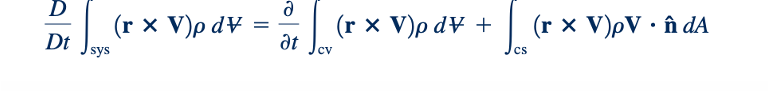
Atau

Untuk suatu volume kontrol yang diam (dan oleh karena itu inersial) dan tidak berubah bentuk, kita menggabungkan Persamaan 5.39, 5.40, dan 5.41 untuk mendapatkan persamaan momen-momentum:

