Perbandingan Persamaan Energi dengan Persamaan Bernoulli
Ketika persamaan energi satu dimensi untuk aliran stabil dalam rata-rata, Persamaan 5.67, diterapkan pada aliran yang stabil, Persamaan 5.67 menjadi persamaan energi aliran satu dimensi dan stabil, Persamaan 5.70.
Satu-satunya perbedaan antara Persamaan 5.67 dan Persamaan 5.70 adalah bahwa daya poros, W, adalah nol jika aliran masuk poros adalah stabil di seluruh volume kontrol (mesin fluida melibatkan aliran lokal yang tidak stabil). Jika selain stabil, aliran tidak dapat dipadatkan, maka dari Persamaan 5.70 kita dapatkan:

Dengan membagi Persamaan 5.72 dengan laju aliran massa, m, dan menyusun ulang suku, kita dapatkan:

Dimana
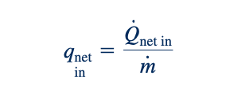
adalah laju transfer panas per laju aliran massa, atau transfer panas per unit massa. Perhatikan bahwa Persamaan 5.73 melibatkan energi per unit massa dan berlaku untuk aliran satu dimensi dari satu aliran fluida antara dua bagian atau aliran sepanjang garis aliran antara dua bagian.
Jika aliran stabil dan tak dapat dipadatkan yang kita pertimbangkan juga melibatkan efek viskositas yang dapat diabaikan (aliran tanpa gesekan), maka persamaan Bernoulli, Persamaan 3.7, dapat digunakan untuk menjelaskan apa yang terjadi antara dua bagian dalam aliran sebagai
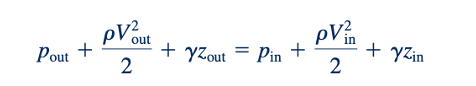
di mana 𝛾 adalah percepatan gravitasi, dan ρg adalah berat jenis fluida. Untuk mendapatkan Persamaan 5.74 dalam bentuk energi per unit massa, sehingga dapat dibandingkan langsung dengan Persamaan 5.73, kita bagi Persamaan 5.74 dengan densitas, ρ, dan kita dapatkan:

Perbandingan Persamaan 5.73 dan 5.75 mendorong kita untuk menyimpulkan bahwa

ketika aliran tak dapat dipadatkan yang stabil tanpa gesekan. Untuk aliran tak dapat dipadatkan yang stabil dengan gesekan, kita mempelajari dari pengalaman (hukum kedua termodinamika) bahwa

Dalam Persamaan 5.73 dan 5.75, kita dapat mempertimbangkan kombinasi variabel
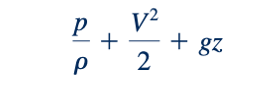
sebagai energi berguna atau tersedia. Dengan demikian, dari inspeksi Persamaan 5.73 dan 5.75, kita dapat menyimpulkan bahwa u˙out − u˙ in + q˙net,in mewakili kerugian energi berguna atau tersedia yang terjadi dalam aliran fluida tak dapat dipadatkan karena gesekan. Dalam bentuk persamaan, kita memiliki:
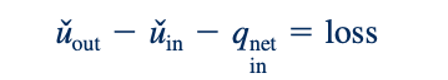
Untuk aliran tanpa gesekan, Persamaan 5.73 dan 5.75 memberitahu kita bahwa kerugian sama dengan nol.
Seringkali nyaman untuk menyatakan Persamaan 5.73 dalam hal kerugian sebagai:

Contoh penerapan Persamaan. 5.79 mengikuti.


Kelompok penting dari masalah mekanika fluida melibatkan aliran satu dimensi, tak dapat dimampatkan, stabil dalam rata-rata dengan gesekan dan kerja poros. Termasuk dalam kategori ini adalah aliran densitas konstan melalui pompa, blower, kipas, dan turbin. Untuk jenis aliran ini, Persamaan 5.67 menjadi:

Membagi Persamaan 5.80 dengan laju aliran massa dan menggunakan pekerjaan per satuan massa, W shaft , net in= W' shaft, net in /m , kita dapatkan:

Jika aliran tetap sepanjang, Persamaan 5.81 menjadi identik dengan Persamaan 5.73, dan pengamatan sebelumnya bahwa u out − u in− q net,in sama dengan kerugian energi yang tersedia berlaku. Dengan demikian, kita menyimpulkan bahwa Persamaan 5.81 dapat dirumuskan sebagai:
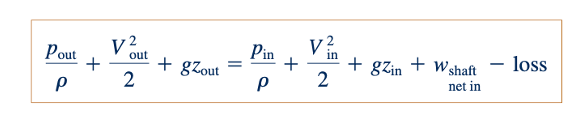
Ini adalah bentuk persamaan energi untuk aliran yang stabil dalam rata-rata yang sering digunakan untuk masalah aliran yang tidak dapat dimampatkan. Kadang-kadang disebut persamaan energi mekanik atau persamaan Bernoulli yang diperluas. Perhatikan bahwa Persamaan 5.82 melibatkan energi per satuan massa (kaki pon detik, slug kaki per detik kuadrat, atau Newton meter kuadrat per meter kuadrat detik kuadrat) (ft.lb/slug = ft2/s2 atau N.m = m2/s2).
Menurut Persamaan 5.82, ketika kerja poros masuk ke dalam volume kontrol, seperti misalnya pada pompa, jumlah kerugian yang lebih besar akan menghasilkan lebih banyak kerja poros yang diperlukan untuk kenaikan energi yang sama. Demikian pula, ketika kerja poros keluar dari volume kontrol (misalnya, turbin), kerugian yang lebih besar akan menghasilkan lebih sedikit kerja poros yang keluar untuk penurunan energi yang sama. Perancang menghabiskan banyak usaha untuk meminimalkan kerugian pada komponen aliran fluida. Contoh-contoh berikut menjelaskan mengapa kerugian harus dijaga sesedikit mungkin dalam sistem fluida.

Jika Persamaan 5.82, yang melibatkan energi per satuan massa, dikalikan dengan kepadatan fluida, ρ, kita mendapatkan:

di mana 𝛾=𝜌𝔤 adalah berat jenis fluida. Persamaan 5.83 melibatkan energi per unit volume dan unit yang terlibat identik dengan yang digunakan untuk tekanan (ft⋅lb/ft 3≡lb/ft 2) atau (N⋅m/m 3 ≡N/m 2).
Jika Persamaan 5.82 dibagi dengan percepatan gravitasi, g, kita mendapatkan:
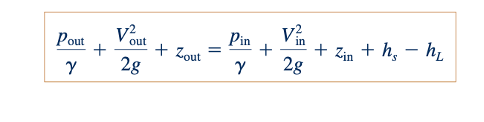
Dimana

hs adalah head kerja poros dan ℎL adalah head loss. Persamaan 5.84 melibatkan energi per unit berat ( ft . lb/lb = ft atau N⋅m/ N=m). Pada Bagian 3.7, kita memperkenalkan konsep "head", yang merupakan energi per unit berat. Satuan panjang (misalnya, ft, m) digunakan untuk mengkuantifikasi jumlah head yang terlibat. Jika sebuah turbin berada dalam volume kontrol, ℎs negatif karena terkait dengan kerja poros keluar dari volume kontrol. Untuk sebuah pompa dalam volume kontrol, ℎs positif karena terkait dengan kerja poros ke dalam volume kontrol.
Kita dapat mendefinisikan total head, H, sebagai berikut:

Maka Persamaan 5.84 dapat dinyatakan sebagai:

Beberapa nilai penting dari H out dibandingkan dengan H in ditunjukkan dalam Gambar 5.8. Perhatikan bahwa hL (kehilangan head) selalu mengurangi nilai H out, kecuali dalam kasus ideal ketika hL adalah nol. Perhatikan juga bahwa hL mengurangi efek dari kerja poros yang dapat diekstraksi dari fluida. Ketika hL=0 (kondisi ideal), head kerja poros, hs, dan perubahan total head adalah sama. Perubahan head ini kadang disebut perubahan head ideal. Head kerja poros ideal yang sesuai adalah yang minimum yang diperlukan untuk mencapai efek yang diinginkan. Untuk kerja keluar, ini adalah maksimum yang mungkin. Para perancang biasanya berusaha untuk meminimalkan kerugian. Di Bab 12 kita mempelajari satu contoh ketika kerugian minimum dikorbankan untuk kelangsungan hidup ikan yang melewati rotor turbin.


