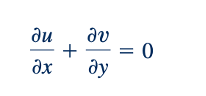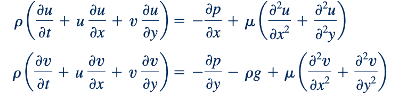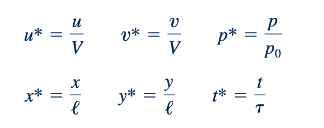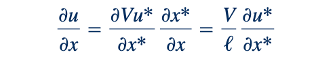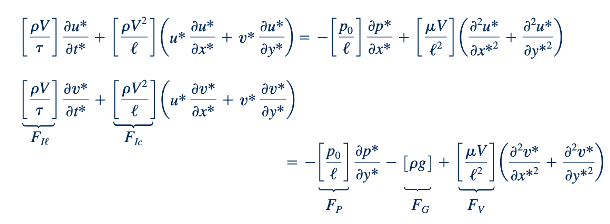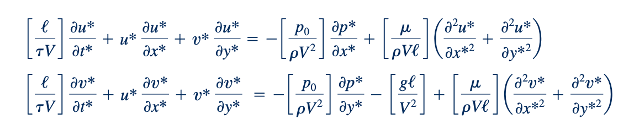Kita melihat bahwa istilah-istilah yang berada dalam tanda kurung adalah kelompok tak berdimensi standar (atau kebalikannya) yang dikembangkan dari analisis dimensional; yaitu, ℓ/𝜏V adalah bentuk dari nomor Strouhal, p0/pV2 adalah nomor Euler, gℓ/V2 adalah kebalikan dari kuadrat nomor Froude, dan 𝜇/pVℓ adalah kebalikan dari nomor Reynolds. Dari analisis ini sekarang jelas bagaimana setiap kelompok tak berdimensi dapat diinterpretasikan sebagai rasio dua gaya, dan bagaimana kelompok-kelompok ini muncul secara alami dari persamaan-persamaan yang mengatur.

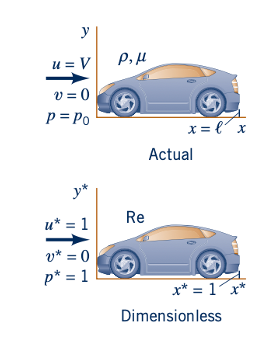
Secara umum, kita belum memberikan bantuan kepada diri kita sendiri dalam memperoleh solusi analitis untuk persamaan-persamaan ini (karena masih rumit dan tidak dapat diurai menjadi solusi analitis), namun bentuk tak berdimensi dari persamaan-persamaan, Eqs. 7.31, 7.34, dan 7.35, dapat digunakan untuk menetapkan persyaratan kesamaan. Dari persamaan-persamaan ini, dapat disimpulkan bahwa jika dua sistem diatur oleh persamaan-persamaan ini, maka solusi-solusi (dalam hal u*, v*, p*, x*, y*, dan t*) akan sama jika empat parameter ℓ/𝜏V, p0 /pV 2, V2g/ℓ dan pVℓ/𝜇 sama untuk kedua sistem tersebut. Dua sistem tersebut akan sama secara dinamis. Tentu saja, kondisi batas dan awal yang diungkapkan dalam bentuk tak berdimensi juga harus sama untuk kedua sistem tersebut, dan ini akan memerlukan kesamaan geometris lengkap. Ini adalah persyaratan kesamaan yang sama yang akan ditentukan oleh analisis dimensional jika variabel-variabel yang sama dipertimbangkan. Namun, keuntungan dari bekerja dengan persamaan-persamaan yang mengatur adalah bahwa variabel-variabel tersebut muncul secara alami dalam persamaan-persamaan, dan kita tidak perlu khawatir akan mengabaikan yang penting, asalkan persamaan-persamaan yang mengatur ditentukan dengan benar. Kita dapat menggunakan metode ini untuk menyimpulkan kondisi di mana dua solusi akan serupa meskipun salah satu solusinya kemungkinan besar akan diperoleh secara eksperimental.


Tingkat tekanan aktual hanya akan penting jika kita peduli dengan kavitasi. Jika tidak, pola aliran dan perbedaan tekanan tidak akan bergantung pada tingkat tekanan. Dalam hal ini, p0 dapat diambil sebagai pV2 (atau 1/2pV2 ), dan bilangan Euler dapat dihilangkan sebagai persyaratan kesamaan. Namun, jika kita peduli tentang kavitasi (yang akan terjadi di lapangan aliran jika tekanan di titik-titik tertentu mencapai tekanan uap, pv2), maka tingkat tekanan aktual penting. Biasanya, dalam kasus ini, tekanan karakteristik, p0, didefinisikan relatif terhadap tekanan uap sehingga p0 = pr - pv di mana pr adalah beberapa tekanan referensi dalam lapangan aliran. Dengan p didefinisikan dengan cara ini, parameter kesamaan p0 menjadi po/ pV2 (pr - pv) / pV2. Parameter ini sering ditulis sebagai (pr - pv)/ 1/2 pV2, dan dalam bentuk ini, seperti yang dicatat sebelumnya dalam Bagian 7.6, disebut sebagai angka kavitasi. Dengan demikian, kita dapat menyimpulkan bahwa jika kavitasi tidak menjadi perhatian kita, kita tidak memerlukan parameter kesamaan yang melibatkan p0, tetapi jika kavitasi harus dimodelkan, maka angka kavitasi menjadi parameter kesamaan penting.

Bilangan Froude, yang muncul karena adanya gravitasi, penting untuk masalah di mana terdapat permukaan bebas. Contoh dari jenis masalah ini termasuk studi sungai, aliran melalui struktur hidrolik seperti saluran air, dan hambatan pada kapal. Dalam situasi ini, bentuk permukaan bebas dipengaruhi oleh gravitasi, dan oleh karena itu bilangan Froude menjadi parameter kesamaan penting. Namun, jika tidak ada permukaan bebas, efek tunggal dari gravitasi adalah menimbulkan distribusi tekanan hidrostatik di atas distribusi tekanan yang dibuat oleh pergerakan fluida. Distribusi hidrostatik dapat dihilangkan dari persamaan yang mengatur 1Persamaan 7.302 dengan mendefinisikan tekanan baru, p' -pgy, dan dengan perubahan ini, bilangan Froude tidak muncul dalam persamaan-persamaan tak berdimensi tersebut.

Kesimpulan dari diskusi ini adalah bahwa untuk aliran fluida tak bergerak dengan permukaan bebas, kesamaan dinamis dan kinematik akan tercapai jika 1untuk sistem yang serupa secara geometri2 kesamaan bilangan Reynolds terwujud. Jika terdapat permukaan bebas, kesamaan bilangan Froude juga harus dipertahankan. Untuk aliran dengan permukaan bebas, kita secara tidak langsung mengasumsikan bahwa tegangan permukaan tidak penting. Namun, kita akan menemukan bahwa jika tegangan permukaan dimasukkan, efeknya akan muncul dalam kondisi batas permukaan bebas, dan bilangan Weber, pV2ℓ/𝜎, akan menjadi parameter kesamaan tambahan. Selain itu, jika persamaan yang mengatur untuk fluida dapat dimampatkan dipertimbangkan, bilangan Mach, V/c, akan muncul sebagai parameter kesamaan tambahan.

Sudah jelas bahwa semua kelompok tak berdimensi yang umum yang sebelumnya kita kembangkan dengan menggunakan analisis dimensional muncul dalam persamaan yang menggambarkan gerakan fluida saat persamaan tersebut dinyatakan dalam variabel tak berdimensi. Oleh karena itu, penggunaan persamaan yang mengatur untuk mendapatkan hukum kesamaan memberikan alternatif untuk analisis dimensional. Pendekatan ini memiliki keuntungan bahwa variabel-variabel tersebut diketahui dan asumsi-asumsi yang terlibat secara jelas teridentifikasi. Selain itu, seringkali dapat diperoleh interpretasi fisik dari berbagai kelompok tak berdimensi.